Все темы ЕГЭ
Меню курса
Об экзамене и примеры задач
В июне 1 кг помидоров стоил 120 рублей. В июле помидоры подешевели на 30%, а в августе еще на 50%. Сколько рублей стал стоить 1 кг помидоров после снижения цены в августе?
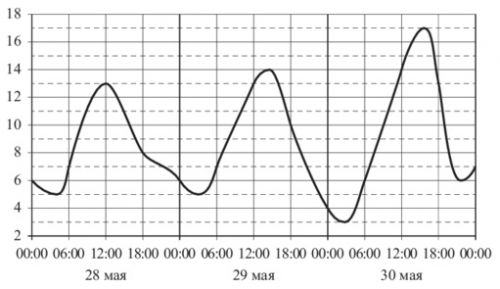
На рисунке показано изменение температуры воздуха на протяжение трёх суток. По горизонтали указывается дата и время, по вертикали - значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 28 мая. Ответ дайте в градусах Цельсия.
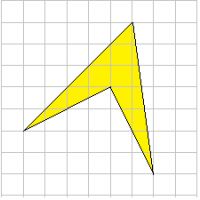
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см.рис.). Ответ дайте в квадратных сантиметрах.
В большой партии светодиодных ламп на каждые 2000 рабочих приходится 7 неисправных. Найдите вероятность того, что случайно выбранная из этой партии лампочка не будет гореть. Ответ округлите до тысячных.
Решите уравнение \(\sqrt{7 - x} = x-5\). Если корней несколько, в ответ запишите меньший из них.
В прямоугольном треугольнике \(ABC\) угол \(C\) равен 90°, \(\sin{B} = \dfrac{5}{13}\). Найдите тангенс внешнего угла при вершине \(A\).
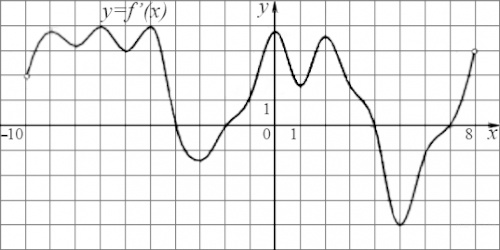
На рисунке изображен график \(y = f’(x)\) - производной функции \(y = f(x)\), определенной на интервале \((-10;8)\). Найдите количество точек максимума функции \(f(x)\), принадлежащих отрезку \([-9;6]\).
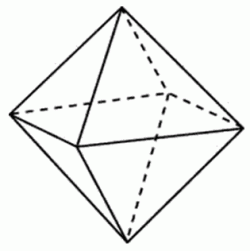
Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?
Найдите \(\log_{a}{(ab^{11})}\), если \(\log_{a}{b} = 5\)
Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры (в кельвинах) от времени работы: \(T(t) = T_0 + bt + at^2\), где \(t\) - время в минутах, \(T_0 = 1320\) К, \(a = -20\) К/мин², \(b = 200\) К/мин. Известно, что при температуре нагревателя свыше \(1800\) К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 8 км/ч большей, чем скорость второго, и прибыл к финишу на 8 часов раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым.
Найдите наименьшее значение функции \(y = 10x - 10\ln(x+3)+ 24\) на отрезке \([-2{,}5; 0]\).
а) Решите уравнение \(4\sin{\left(x - \dfrac{7\pi}{2}\right)} = \dfrac{3}{\cos{x}}\)
б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{13\pi}{2};-5\pi\right]\)
Запишите номера всех верных ответов на пункты а) и б) по возрастанию, через запятую, без пробелов. В первое поле на пункт а), во второе - на пункт б)
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -13π/2 | 18. -19π/3 | 19. -25π/4 | 20. -37π/6 |
| 21. -6π | 22. -35π/6 | 23. -23π/4 | 24. -17π/3 |
| 25. -11π/2 | 26. -16π/3 | 27. -21π/4 | 28. -31π/6 |
| 29. -5π |