Тела вращения

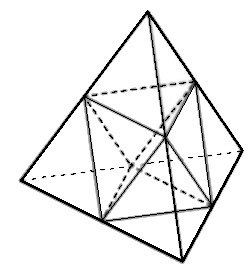
Объём тетраэдра равен 15. Найдите объём многогранника, вершинами которого являются середины рёбер данного тетраэдра.

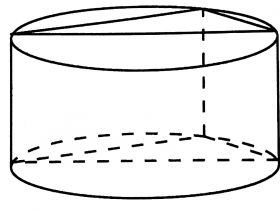
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объем параллелепипеда.

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра призмы равны 2/π. Найдите объём цилиндра, описанного около этой призмы.

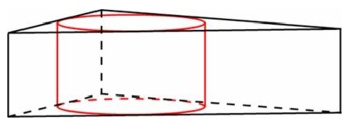
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.

Объем первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания – в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.

В цилиндрический сосуд налили 2300 cм³ воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см³

Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.

Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.

​

В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.

Найдите объем правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота √3.

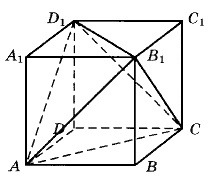
Объем параллелепипеда ABCDA₁B₁C₁D₁ равен 18. Найдите объем треугольной пирамиды AD₁CB₁.

​

Прямоугольный параллелепипед описан около сферы радиуса 5. Найдите его объем.

Площадь большого круга шара равна 5. Найдите площадь поверхности шара.

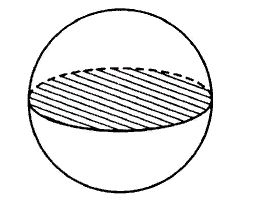
Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.

Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 12 раз?

Во сколько раз увеличится объем шара, если его диаметр увеличить в 5 раз?

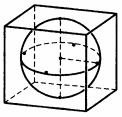
Шар, объём которого равен 6π, вписан в куб. Найдите объём куба.

Цилиндр описан около шара. Объем цилиндра равен 27. Найдите объем шара.

Куб вписан в шар радиуса √3 . Найдите объем куба.

Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём конуса, если объём цилиндра равен 24.

Объем конуса равен 48. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Во сколько раз уменьшится объем конуса, если его высота уменьшится в 4 раза, а радиус основания останется прежним?

Длина окружности основания конуса равна 6, образующая равна 7. Найдите площадь боковой поверхности конуса.

Даны два конуса. Образующая второго конуса в 3 раза больше, чем образующая первого, а радиусы основания у них одинаковые. Во сколько раз площадь боковой поверхности второго конуса больше, чем площадь боковой поверхности  первого?

Образующая конуса равна 18, диаметр основания равен 14. Найдите площадь полной поверхности конуса, деленную на π.

Площадь полной поверхности конуса равна 16. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

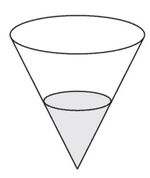
В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 30 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Площадь основания конуса равна 16π, высота – 6. Найдите площадь осевого сечения конуса.

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 3√2. Найдите площадь боковой поверхности конуса.

Радиусы двух шаров равны 5 и 12. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей данных шаров.

Куб, площадь поверхности которого равна 288, вписан в шар. Найдите объем этого шара, деленный на π.

В цилиндрический сосуд налили \(\dfrac{9604}{\sqrt{\pi}}\,см^3\) воды. Уровень жидкости при этом достиг 21см. Затем, в него опустили шар, который целиком скрылся под водой, и уровень жидкости поднялся на 1см. Найдите площадь поверхности этого шара. Ответ выразите в \(см^2\).

В правильной треугольной призме все рёбра равны 2. Точка M — середина ребра AA₁.
а) Докажите, что прямые MB и B₁C перпендикулярны.
б) Найдите расстояние между прямыми MB и B₁C.