9 вариант ЕГЭ Ященко 2025

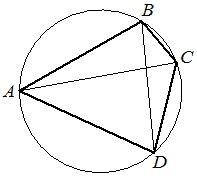
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 73°, угол CAD равен 55°. Найдите угол ABC. Ответ дайте в градусах.

Даны векторы \(\vec{a}(-6;-8)\) и \(\vec{b}(12;9)\). Найдите косинус угла между ними.

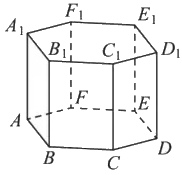
Найдите объём многогранника, вершинами которого являются точки A, B, D, E₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 18, а боковое ребро равно 6.

В чемпионате по гимнастике участвуют 50 спортсменов: 17 из Перу, 22 из Чили, остальные из Мексики. Порядок, в котором выступают гимнасты, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Мексики.

Из 10 билетов 2 являются выигрышными. Наугад берут 4 билета. Найдите вероятность того, что среди них окажется ровно один выигрышный. Ответ округлите до сотых.

Найдите корень уравнения \(\log_2(4-5x)=3\log_23\)

Найдите значение выражения \(5\sin\dfrac{7π}{12}\cdot\cos\dfrac{7π}{12}\)

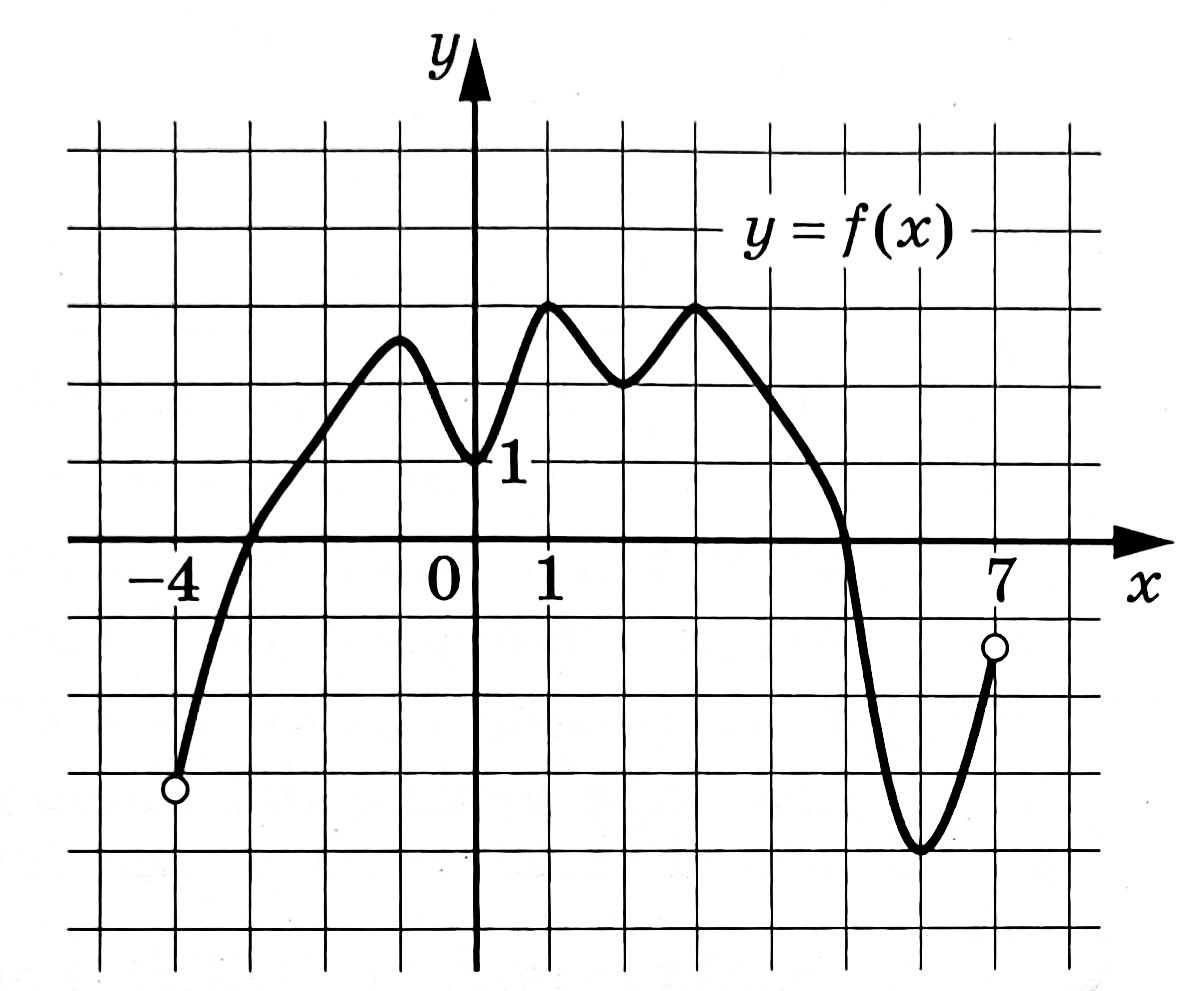
На рисунке изображён график функции y=f(x), определённый на интервале (-4;7). Определите количество точек, в которых производная функции f(x) равна 0.

На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: \(F_A=ρgl^3\), где \(ρ=1000\) кг/м³ — плотность воды, \(g\) — ускорение свободного падения (считайте \(g=9,8\) Н/кг), а \(l\) — длина ребра куба в метрах. Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше чем 893 025 Н? Ответ дайте в метрах.

Двое рабочих, работая вместе, могут выполнить работу за 9 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 2 дня выполняет такую же часть работы, какую второй — за 3 дня?

Найдите точку максимума функции \(y=(2x-3)\cos x-2\sin x+17\) на промежутке \(\left(0;\dfrac{π}{2}\right)\)

а) Решите уравнение \(\sqrt{4x^2-1}\cdot\left(4^{3x+1}-26\cdot8^x+12\right)=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([-1;1]\)

а) В правильной пирамиде SABC с вершиной S на стороне основания AC и боковом ребре SB отметили соответственно точки E и N такие, что AE:EC =SN:NB =1:2. Через точки E и N параллельно прямой AB провели плоскость α.
а) Докажите, что сечением пирамиды SABC плоскостью α является равнобедренная трапеция.
б) Плоскость α разделила пирамиду SABC на два многогранника. Найдите объём того из них, в котором одной из вершин является точка A, если AB=6, AS=3√3.

Решите неравенство \(x^2\cdot\log_{125}(2-3x)+\log_{0{,}2}(9x^2-12x+4)<0\)

В июле 2029 года планируется взять кредит на 5 лет в размере 910 тыс. рублей. Условия его возврата таковы:
- каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле 2030 и 2031 годов долг остаётся равным 910 тыс. рублей;
- выплаты в 2032, 2033 и 2034 годах равны;
- к июлю 2034 года долг будет выплачен полностью.
Найдите общую сумму выплат по кредиту.

В квадрате ABCD на диагонали BD и на сторонах AB и BC отметили соответственно точки P, E и F такие, что BE=BF, а прямая, проходящая через точку P параллельно прямой AC, отсекает от квадрата треугольник, площадь которого равна площади четырёхугольника EBFP и в четыре раза меньше площади квадрата.
а) Докажите, что если BP·BE=√2, то AB=2.
б) Найдите отношение площадей треугольников EPF и EBF.

Найдите все a, при которых система \(\begin{cases} \sqrt{a+x^2}=\sqrt{a+y^2},\\x^2+y^2=2x+2|y|+4\end{cases}\) имеет ровно два решения.

Дан набор натуральных чисел, каждое из которых меньше 100 и записано с помощью цифр 1, 3, 5, 7 или 9. В наборе есть хотя бы одно однозначное и хотя бы одно двузначное число. Из этого набора чисел получили второй набор чисел следующим образом:
– к каждому однозначному числу приписали цифру, с помощью которой это число было записано;
– вместо каждого двузначного числа записали среднее арифметическое двух его цифр.
а) Может ли сумма чисел первого набора быть на 6 меньше суммы чисел второго набора?
б) Может ли сумма чисел первого набора быть в два раза больше суммы чисел второго набора?
в) Найдите наибольшее возможное отношение суммы чисел второго набора к сумме чисел первого набора, если в первом наборе не было одинаковых чисел, а однозначных чисел было столько же, сколько и двузначных.

Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.