36 вариантов ЕГЭ 2025
Меню курса
7 вариант ЕГЭ Ященко 2025
Площадь параллелограмма равна 180, две его стороны равны 60 и 80. Найдите меньшую высоту этого параллелограмма.
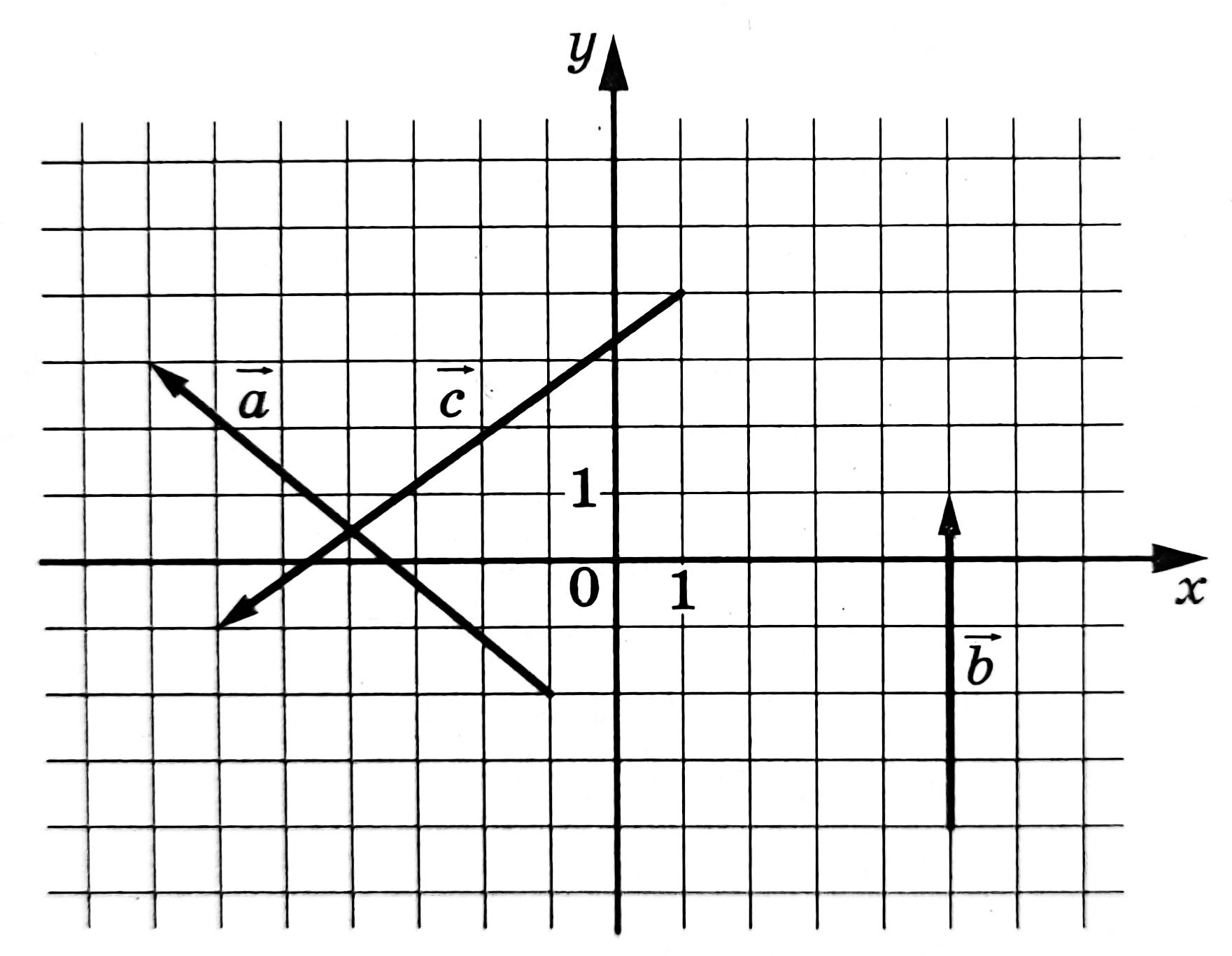
На координатной плоскости изображены векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\), координаты этих векторов - целые числа. Найдите скалярное произведение векторов \(\vec{a}\cdot(\vec{b}+\vec{c})\)
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 24. Найдите площадь поверхности шара.
За круглый стол на 11 стульев в случайном порядке рассаживаются 9 мальчиков и 2 девочки. Найдите вероятность того, что между двумя девочками будет сидеть один мальчик.
Игральный кубик бросают два раза. Во сколько раз вероятность события "выпадет разное количество очков" больше вероятности события "выпадет одинаковое количество очков"?
Найдите корень уравнения \(\sqrt{\dfrac{32}{3x-4}}=1{,}6\). Если уравнение имеет несколько корней, в ответ запишите меньший из них.
Найдите значение выражения \(8^{0{,}24}\cdot16^{0{,}32}\)
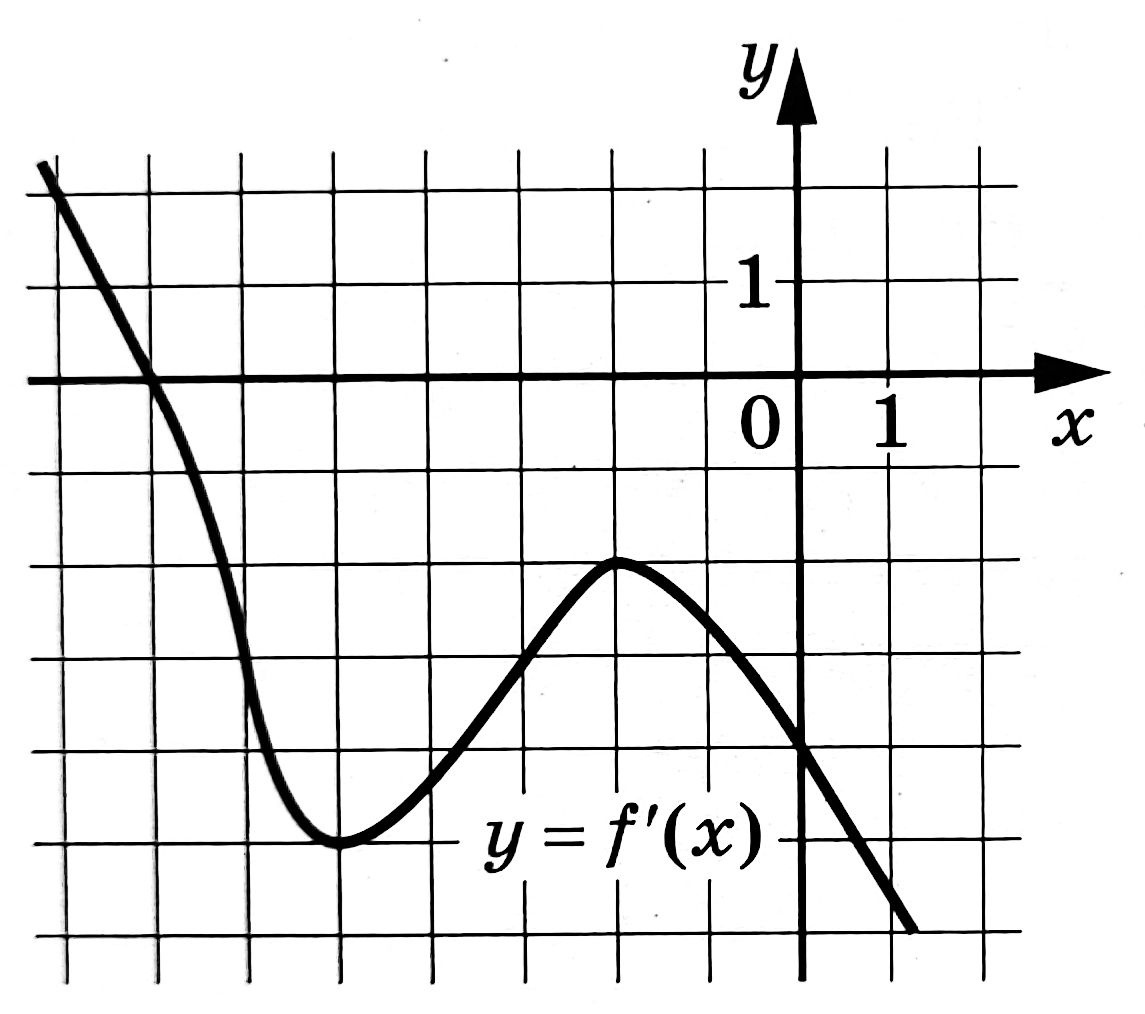
На рисунке изображён график y=f'(x) - производной функции f(x). Найдите абсциссу точки, принадлежащей отрезку [-8;1], в которой касательная к графику y=f(x) параллельна оси абсцисс или совпадает с ней.
После дождя уровень воды в колодце может повыситься. Мальчик измеряет время \(t\) падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле \(h=5t^2\), где \(h\) - расстояние в метрах, \(t\) - время падения в секундах. До дождя время падения камешков составляло 1,3 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
Имеется два сплава. Первый содержит 5% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 125 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
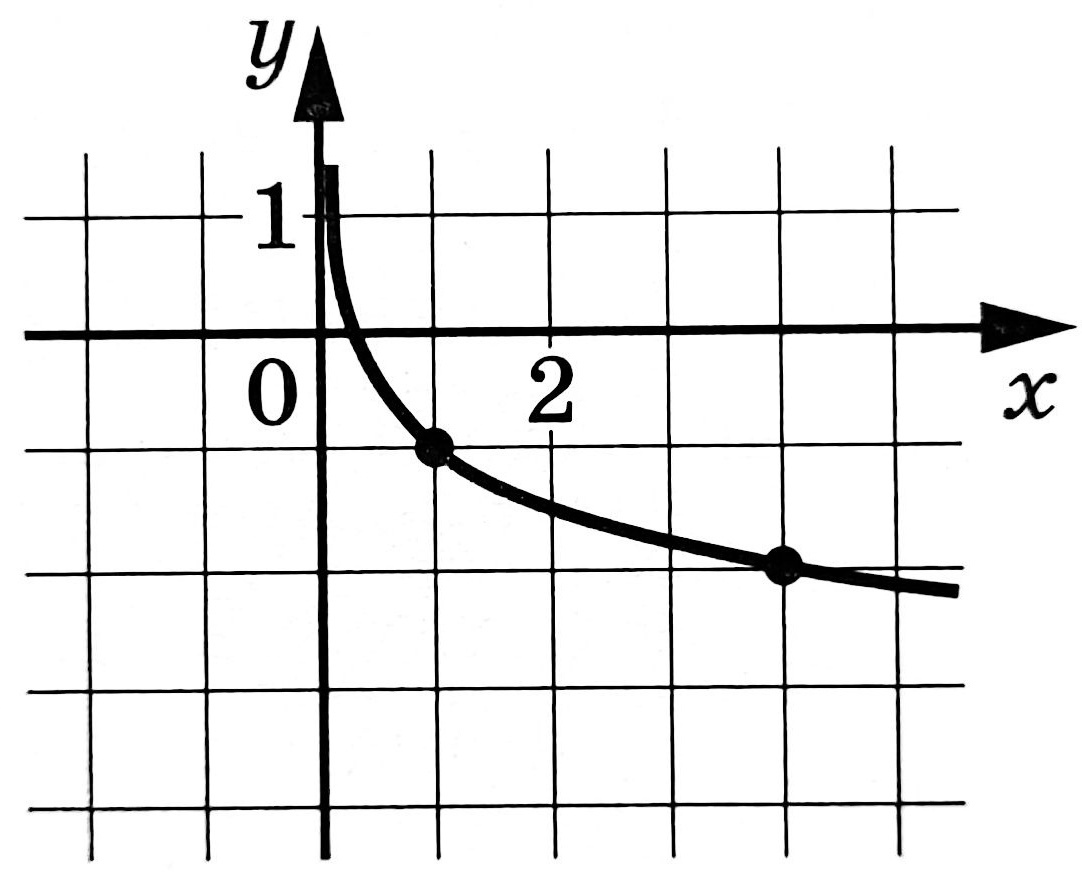
На рисунке изображён график функции \(f(x)=c+\log_ax\). Найдите \(f(64)\)
Найдите наименьшее значение функции \(y=\dfrac{2x^2-9x+8}{x}\) на отрезке [0,5;10].
а) Решите уравнение \(\dfrac{4\sin^3x-2\sin x}{\sin(2x-\pi)}=1\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-3\pi;-\dfrac{\pi}2\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -3π | 18. -17π/6 | 19. -11π/4 | 20. -8π/3 |
| 21. -5π/2 | 22. -7π/3 | 23. -9π/4 | 24. -13π/6 |
| 25. -2π | 26. -11π/6 | 27. -7π/4 | 28. -5π/3 |
| 29. -3π/2 | 30. -4π/3 | 31. -5π/4 | 32. -7π/6 |
| 33. -π | 34. -5π/6 | 35. -3π/4 | 36. -2π/3 |
| 37. -π/2 |
В правильной призме ABCA₁B₁C₁ сторона AB основания ABC равна 4, а боковое ребро AA₁ равно 6. На рёбрах BB₁, CC₁ и A₁B₁ соответственно отмечены точки N, K и P так, что CK:KC₁=B₁N:NB=B₁P:PA₁=1:2. Плоскость KNP пересекает ребро A₁C₁ в точке F.
а) Докажите, что точка F — середина ребра A₁C₁.
б) Найдите расстояние от точки F до плоскости ANK.
Решите неравенство \(\dfrac{16^{x+0{,}5}-4^{x+1{,}5}-4}{4^x-2}+\dfrac{100}{4^x-8}\geqslant4^{x+1}-24\)
В июле 2029 года планируется взять кредит в банке на 2 млн рублей на 4 года. Условия его возврата таковы:
- каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле 2030, 2031 и 2032 годов долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
- в июле 2033 года выплачивается остаток по кредиту в размере 406 тыс. рублей.
Найдите r, если общая сумма выплат по кредиту составит 2752 тыс. рублей.
В треугольнике ABC точки N и P — середины сторон AB и BC соответственно. Отрезок NP касается окружности, вписанной в треугольник ABC.
а) Докажите, что периметр треугольника ABC равен 4AC.
б) Найдите площадь треугольника ABC, если его периметр равен 28, ∠BAC=120°.
Найдите все значения \(a\), при каждом из которых система неравенств \(\begin{cases}(a-x)^2+(y+a)^2\leqslant a+3\\x-y\leqslant|3-2a|\end{cases}\) имеет единственное решение.
Есть 2 камня, каждый массой 100 тонн, 6 камней, каждый массой 20 тонн, и 4 камня, каждый массой 4 тонны.
а) Можно ли разложить все эти камни на три группы так, чтобы суммарная масса первой группы была на 12 тонн больше суммарной массы второй группы, но на 12 тонн меньше суммарной массы третьей группы?
б) Можно ли разложить все эти камни на три группы так, чтобы суммарные массы этих групп были равны?
в) Все камни хотят разложить на три группы с суммарными массами \(m_1\), \(m_2\) и \(m_3\) так, что \(m_1\geqslant m_2\geqslant m_3\). Найдите наименьшее такое число \(d\), что \(m_1-m_2\leqslant d\) и \(m_2-m_3\leqslant d\)
Введите ответ в форме строки "да;да;12". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.