Разные задачи
- 1. Чётность
- 2. Делимость
- 3. Игры
- 4. Комбинаторика
- 5. Текстовые задачи
- 6. Вычисления
- 7. Уравнения
- 8. Планиметрия
- 9. Стереометрия
- 10. Матрицы
-
11. Устаревшие задачи ЕГЭ и ОГЭ
- 11.1. Простые текстовые задачи
- 11.2. Графики и диаграммы
- 11.3. Упрощение выражений
- 11.4. Анализ данных
- 11.5. Анализ графиков
- 11.6. Задачи на проценты и пропорции
- 11.7. Анализ диаграмм
- 11.8. Практические задачи по геометрии
- 11.9. Практическая задача II
- 11.10. Практическая задача III
- 11.11. Практическая задача IV
- 11.12. Практическая задача V
- 12. Натуральные числа
- 13. Теория вероятностей
- 14. Сканави
- 15. ВПР
Задача №6733
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт. Петя и Вася сумели измерить расстояние между концами соседних спиц \(a\). Оно оказалось равно 38 см. Высота купола зонта \(h\) (рис. 2) оказалась равна 25 см, а расстояние \(d\) между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 100 см.
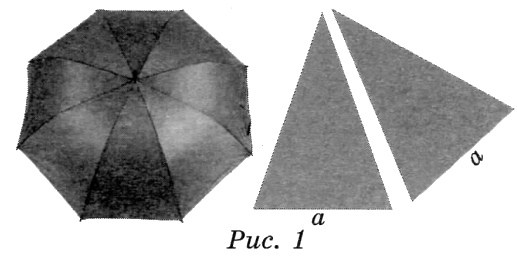
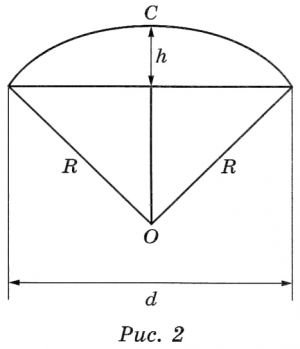
Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле \(S = 2\pi Rh\)‚ где \(R\) – радиус сферы, а \(h\) – высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число \(\pi\) округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.