36 вариантов ЕГЭ 2021
Меню курса
4 вариант ЕГЭ Ященко с решением
В летнем лагере 220 детей и 24 воспитателя. Автобус рассчитан не более чем на 38 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?
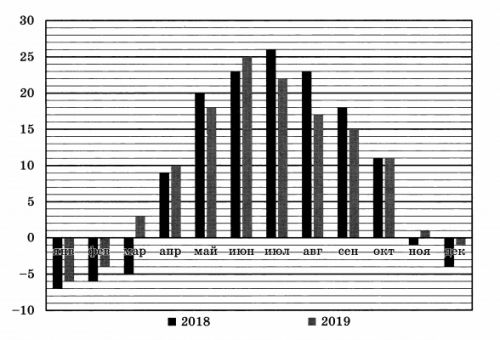
На диаграмме показано изменение средней температуры за каждый месяц в 2018 и 2019 годах в Волгограде. По горизонтали указаны месяцы, по вертикали – значение температуры в градусах Цельсия. Определите разницу между наибольшей и наименьшей среднемесячными температурами в Волгограде в 2019 году. Ответ дайте в градусах Цельсия.
На клетчатой бумаге с размером клетки 1×1 изображен квадрат. Найдите радиус вписанной в него окружности.

Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей – 1 очко, если проигрывает – 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований, если вероятности выигрыша и проигрыша в каждой игре одинаковы и равны 0,4.
Найдите корень уравнения \(\log_{0{,}5}{(x+5)} = \log_{2}{0{,}2}\).
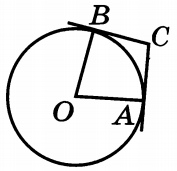
Через концы A и B дуги окружности с центром O проведены касательные CA и CB. Угол CAB равен 39°. Найдите угол AOB. Ответ дайте в градусах.
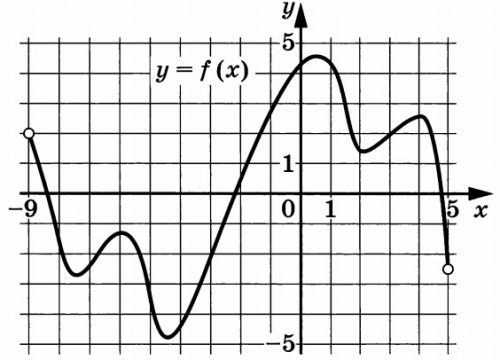
На рисунке изображен график функции \(y = f(x)\), определенной на интервале \((-9; 5)\). Найдите количество точек, в которых производная функции \(f(x)\) равна 0.
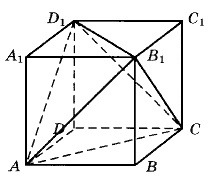
Объём параллелепипеда ABCDA₁B₁C₁D₁ равен 60. Найдите объём треугольной пирамиды ACB₁D₁.
Найдите значение выражения \(\dfrac{{14}^{6{,}4} \cdot 7^{-5{,}4}}{4^{2{,}2}}\)
Мяч бросили под острым углом \(\alpha\) к плоскости горизонтальной поверхности земли. Время полёта мяча (в секундах) определяется по формуле \(t = \dfrac{2v_0 \sin{\alpha}}{g}\). При каком значении угла \(\alpha\) (в градусах) время полета составит \(1{,}4\) секунды, если мяч бросают с начальной скоростью \(v_0 = 14\) м/с. Считайте, что ускорение свободного падения \(g = 10\) м/с².
Смешали 3 кг 24-процентного раствора, 4 кг 32-процентного раствора и некоторое количество 48-процентного раствора одного и того же вещества. Сколько килограммов 48-процентного раствора использовали, если в результате получили 40-процентный раствор вещества?
Найдите точку минимума функции \(y = (x+4)^2(x+1) + 9\).
a) Решите уравнение \((x^2 + 4x - 2)(4^{3x+1} + 8^{2x-1} - 11) = 0\)
б) Найдите все корни уравнения, принадлежащие отрезку \([-0{,}5; 0{,}5]\)
В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 8, а боковое ребро SA равно 7. На рёбрах AB и SB отмечены точки M и K соответственно, причем AM = 2, SK = 1. Плоскость \(\alpha\) перпендикулярна плоскости ABC и содержит точки M и K.
а) Докажите, что плоскость \(\alpha\) содержит точку C.
б) Найдите площадь сечения пирамиды SABCD плоскостью \(\alpha\).
Решите неравенство \(\lg^4(x^2-26)^4-4\lg^2(x^2-26)^2\leqslant240\)
В четырёхугольнике ABCD противоположные стороны не параллельны. Диагонали четырёхугольника ABCD пересекаются в точке O под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин – точка O.
а) Докажите, что в четырехугольник ABCD можно вписать окружность.
б) Найдите радиус вписанной окружности, если AC = 12, BD = 13.
Виктор планирует 15 декабря взять в банке кредит на 2 года в размере 1962000 рублей. Сотрудник банка предложил Виктору два различных варианта погашения кредита, описание которых приведено в таблице.
| Вариант 1 |
– каждый январь долг возрастает на 18% по сравнению с концом предыдущего года; |
| Вариант 2 | – 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; – со 2-го по 14-е число каждого месяца необходимо выплатить часть долга – 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца; – к 15-му числу 24-го месяца кредит должен быть полностью погашен |
На сколько рублей меньше окажется общая сумма выплат банку по более выгодному для Виктора варианту погашения кредита?
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases} y + 2 - \dfrac{4}{x} = \left|y + \dfrac{2}{x} - 3 \right| \\ 2y(y+2) + 3x(ax - 2) = xy(2a+3) \end{cases}\) имеет более 3 решений.
Оля участвовала в викторине по истории. За каждый правильный ответ участнику начисляется 8 баллов, за каждый неверный – списывается 8 баллов, за отсутствие ответа списывается 3 балла. По результатам викторины Оля набрала 35 баллов.
а) На сколько вопросов Оля ответила правильно, если в викторине было 24 вопроса?
б) На сколько вопросов Оля не дала ответа, если в викторине было 25 вопросов?
в) На сколько вопросов Оля ответила неверно, если в викторине было 37 вопросов?
Введите ответ в форме строки "21;43;7", где ответы на пункты разделены ";".