36 вариантов ЕГЭ 2021
Меню курса
14 вариант ЕГЭ Ященко с решением
Налог на доходы составляет \(13\%\) от заработной платы. После удержания налога на доходы Мария Константиновна получила \(15660\) рублей. Сколько рублей составляет заработная плата Марии Константиновны?
На рисунке показана средняя цена свинца во все месяцы 2017 и 2018 годов. По горизонтали указаны месяцы, по вертикали — цена тонны свинца в долларах США. Для наглядности точки соединены отрезками.
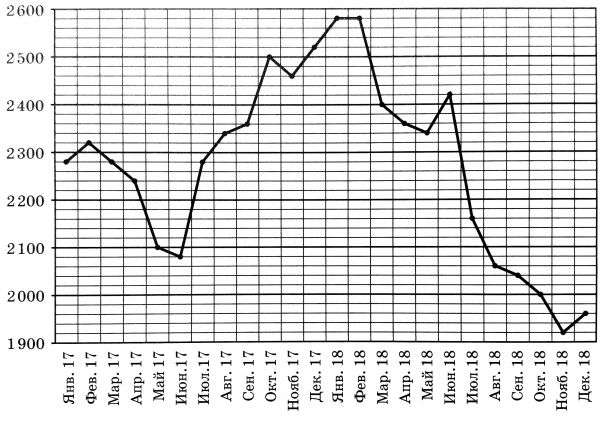
Определите по рисунку цену тонны свинца в июне 2018 года.
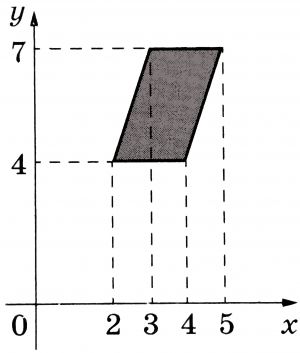
Найдите площадь параллелограмма, изображённого на рисунке.
Игральную кость бросают дважды. Найдите вероятность того, что произведение выпавших очков делится на 3. Ответ округлите до тысячных.
Найдите корень уравнения \(\sqrt{2x-3}=x-3 \). Если уравнение имеет более одного корня, в ответе запишите наименьший из корней.
Два угла вписанного в окружность четырёхугольника равны 112° и 125°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
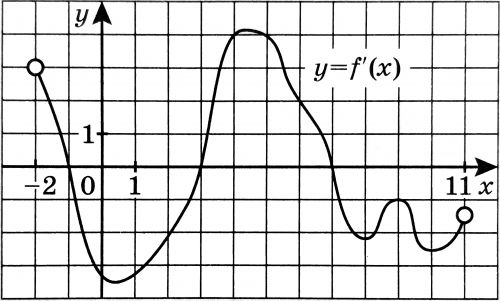
На рисунке изображён график \(y=f'(x)\) производной функции \(f(x)\), определённой на интервале \((-2; 11)\). Найдите количество точек, в которых касательная к графику функции \(f(x)\) параллельна прямой \(y=-2x-5\) или совпадает с ней.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём конуса равен 19. Найдите объём шара.
Найдите \(\log_{a}{(a^4b^3)}\), если \(\log_{a}{b}=4\)
При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу, частота звукового сигнала, регистрируемого приёмником, не совпадает с частотой исходного сигнала \(f_0=130\,Гц\) и определяется следующим выражением: \(f=f_0\dfrac{c+u}{c-v}\,(Гц)\), где \(c\) - скорость распространения сигнала в среде (в м/с), а \(u=15\) м/с и \(v=9\)м/с - скорости приёмника и источника относительно среды соответственно. При какой максимальной скорости \(c\) (в м/с) распространения сигнала в среде частота сигнала в приёмнике \(f\) будет не менее \(135\, Гц\)?
Из одной точки круговой трассы, длина которой равна 25 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 114 км/ч, и через 30 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Найдите наименьшее значение функции \(y=(1-x)e^{2-x}\) на отрезке \([0{,}5; 5]\).
а) Решите уравнение \(\log_{\frac{1}{3}}\left({2\sin^2x-3\cos2x+6}\right)=-2\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{7\pi}{2};-2\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4.π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -7π/2 | 18. -10π/3 | 19. -13π/4 | 20. -19π/6 |
| 21. -3π | 22. -17π/6 | 23. -11π/4 | 24. -8π/3 |
| 25. -5π/2 | 26. -7π/3 | 27. -9π/4 | 28. -13π/6 |
| 29. -2π |
В правильной треугольной усечённой пирамиде \(ABCA_1B_1C_1\) площадь нижнего основания \(ABC\) в девять раз больше площади меньшего основания \(A_1B_1C_1\). Через ребро \(AB\) проведена плоскость \(\alpha\), которая пересекает ребро \(CC_1\) в точке \(N\) и делит пирамиду на два многогранника равного объёма.
а) Докажите, что точка \(N\) делит ребро \(CC_1\) в отношении \(5 : 13\), считая от точки \(C_1\).
б) Найдите площадь сечения усечённой пирамиды плоскостью \(\alpha\), если высота пирамиды равна 13, а ребро меньшего основания равно 3.
Решите неравенство \(3\cdot25^{x+0{,}5}+4^{2x+1{,}5}\leqslant22\cdot20^{x}\)
Окружность проходит через вершины \(A\), \(B\) и \(D\) параллелограмма \(ABCD\), пересекает сторону \(BC\) в точках \(B\) и \(M\), а также пересекает продолжение стороны \(CD\) за точку \(D\) в точке \(N\).
а) Докажите, что \(AM=AN\)
б) Найдите отношение \(CD:DN\), если \(AB:BC=2:3\), а \(\cos\angle BAD=0{,}7\)
Ответ запишите в виде несократимого отношения без пробелов, например "4:13".
В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
- каждый январь долг возрастает на 16% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга, равную 2,523 млн рублей.
Сколько миллионов рублей было взято в банке, если известно, что он был полностью погашен двумя равными платежами (то есть за два года)?
Найдите все значения параметра \(a\), при которых система уравнений
\(\begin{cases}\dfrac{(y-\sqrt{10-x^2})\left((x+5)^2+(y+5)^2-10(x+7{,}5)+x^2-y^2+5\right)}{\sqrt{x^2-1}}=0\\y=ax+a-1\end{cases}\)
имеет одно решение.
В школах №1 и №2 учащиеся писали тест. Из каждой школы тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе №1 уменьшиться в 10 раз?
б) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе №2 равняться 7?
в) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе №2.
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.