36 вариантов ЕГЭ 2021
Меню курса
29 вариант ЕГЭ Ященко с решением
В июле на рынке голландские помидоры стоили на 25% дешевле краснодарских; в августе они подорожали на 10%, а краснодарские помидоры подешевели на 40% за счёт сезонного падения цен. На сколько процентов голландские помидоры дороже краснодарских в августе?
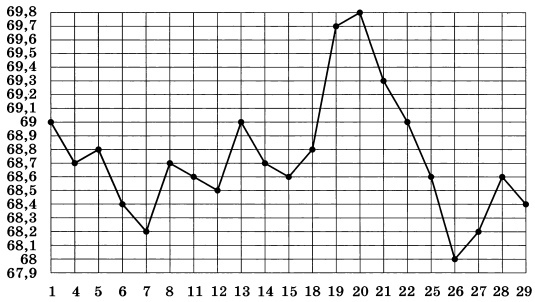
На графике жирными точками показан курс евро, установленный Центробанком РФ, на все рабочие дни с 1 сентября по 29 сентября 2017 года. По горизонтали указываются числа месяца, по вертикали - цена евро в рублях. Для наглядности точки соединены линиями. Определите наименьший курс евро в рублях в период с 5 по 18 сентября.
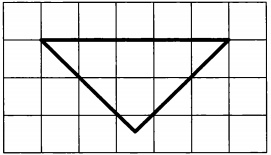
На клетчатой бумаге с размером клетки 1×1 изображён равнобедренный прямоугольный треугольник. Найдите длину его медианы, проведённой к гипотенузе.
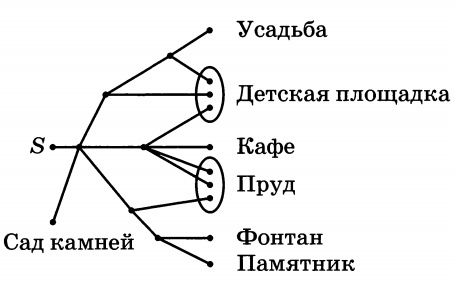
Артём гуляет по парку. Он выходит из точки S и, дойдя до очередной развилки, с равными шансами выбирает следующую дорожку, но не возвращается обратно. Найдите вероятность того, что таким образом он выйдет к пруду или фонтану.
Найдите корень уравнения \(\log_{7}{(x+8)}=1+\log_{7}{(3x-14)}\)
Около окружности описана трапеция, периметр которой равен 28. Найдите длину её средней линии.
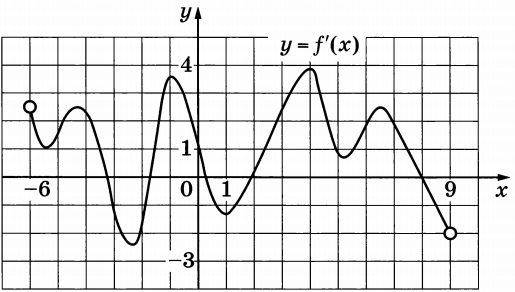
На рисунке изображён график \(y=f'(x)\) – производной функции \(f(x)\), определённой на интервале (-6; 9). Найдите количество точек максимума функции \(f(x)\), принадлежащих отрезку [-3; 7].
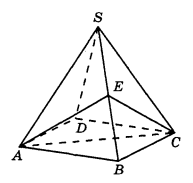
Объем правильной четырехугольной пирамиды SABCD равен 52. Точка Е – середина ребра SB. Найдите объем треугольной пирамиды ЕАВС.
Найдите значение выражения \(\dfrac{\sqrt[5]{45}\cdot\sqrt[5]{189}}{\sqrt[5]{35}}\)
Для определения эффективной температуры звёзд используют закон Стефана-Больцмана, согласно которому \(P=σST^4\), где \(P\) — мощность излучения звезды (в Вт), \(σ=5{,}7\cdot 10^{-8}\, \dfrac{Вт}{м^2\cdot K^4}\) – постоянная, \(S\) – площадь поверхности звезды \((в\,м^2)\), а \(T\) – температура (в К). Известно, что площадь поверхности некоторой звезды равна \(\dfrac{1}{256}\cdot 10^{11}\, (м^2)\), а мощность её излучения равна \(4,617\cdot 10^{13}\) Вт. Найдите температуру этой звезды. Ответ дайте в Кельвинах.
Имеется два сплава. Первый сплав содержит 15% меди, второй - 40% меди. Масса второго сплава больше массы первого на 45 кг. Из этих двух сплавов получили третий сплав, содержащий 35% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Найдите точку максимума функции \(y=2x^2-57x+203\ln{x}+28\)
а) Решите уравнение \(2\sin2x-4\cos x+3\sin x-3=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\pi; \dfrac{5\pi}2\right]\)
Запишите номера всех верных ответов на пункты а) и б) по возрастанию, через запятую, без пробелов. В первое поле на пункт а), во второе - на пункт б)
а)
| 1. \(2\pi n,\; n\in\mathbb{Z}\) | 2. \(\dfrac{\pi}{6}+2\pi n,\; n\in\mathbb{Z}\) | 3. \(\dfrac{\pi}{4}+2\pi n,\; n\in\mathbb{Z}\) | 4. \(\dfrac{\pi}{3}+2\pi n,\; n\in\mathbb{Z}\) |
| 5. \(\dfrac{\pi}{2}+2\pi n,\; n\in\mathbb{Z}\) | 6. \(\dfrac{2\pi}{3}+2\pi n,\; n\in\mathbb{Z}\) | 7. \(\dfrac{3\pi}{4}+2\pi n,\; n\in\mathbb{Z}\) | 8. \(\dfrac{5\pi}{6}+2\pi n,\; n\in\mathbb{Z}\) |
| 9. \(\arccos3/4+2\pi n,\; n\in\mathbb{Z}\) | 10. \(\arccos(-3/4)+2\pi n,\; n\in\mathbb{Z}\) | 11. \(-\arccos3/4+2\pi n,\; n\in\mathbb{Z}\) | 12. \(-\arccos(-3/4)+2\pi n,\; n\in\mathbb{Z}\) |
б)
| 13. π | 14. 7π/6 | 15. 5π/4 | 16. 4π/3 |
| 17. 3π/2 | 18. 5π/3 | 19. 7π/4 | 20. 11π/6 |
| 21. 2π | 22. 13π/6 | 23. 9π/4 | 24. 7π/3 |
| 25. 5π/2 | 26. \(\pi+\arccos3/4\) | 27. \(2\pi-\arccos3/4\) | 28. \(2\pi+\arccos3/4\) |
Точки A, B и C лежат на окружности основания конуса с вершиной S, причём A и C диаметрально противоположны. Точка M – середина BC.
а) Докажите, что прямая SM образует с плоскостью ABC такой же угол, как и прямая AB с плоскостью SBC.
б) Найдите угол между прямой SA и плоскостью SBC, если AB=6, BC=10 и SC=4√3
Решите неравенство \(\dfrac{2^x}{2^x-3}+\dfrac{2^x+1}{2^x-2}+\dfrac{5}{4^x-5\cdot 2^x +6}\leqslant 0\)
Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK=3 и MK=12.
1 января 2015 года Иван Сергеевич взял в банке 1 млн рублей в кредит. Схема выплаты кредита следующая:
– 1 числа каждого следующего месяца банк начисляет 2% на оставшуюся сумму долга (то есть, увеличивает долг на 2%);
– затем Иван Сергеевич переводит в банк очередной платеж.
На какое минимальное количество месяцев Иван Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 200 тысяч рублей?
Найдите все значения \(a\), при каждом из которых множество значений функции \(y=\dfrac{5a+150x-10ax}{100x^2+20ax+a^2+25}\) содержит отрезок [0;1].
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы в каждой группе было хотя бы одно число. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы из единственного числа среднее арифметическое равно этому числу).
а) Могут ли быть одинаковыми два из этих трёх значений средних арифметических в группах из разного количества чисел?
б) Могут ли быть одинаковыми все три значения средних арифметических?
в) Найдите наименьшее возможное значение наибольшего из получаемых трёх средних арифметических.
Введите ответ в форме строки "да;да;23:34", где ответы на пункты разделены ";", первые два ответа с маленькой буквы, а ответ на пункт в) в виде не сократимого отношения, записанного через ":".