36 вариантов ЕГЭ 2021
Меню курса
6 вариант ЕГЭ Ященко с решением
Бегун пробежал 500 метров за 1 минуту 20 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной - давление в миллиметрах ртутного столба. Определите, используя график, на сколько высота над уровнем моря при атмосферном давлении 320 мм рт. ст. больше, чем при атмосферном давлении 540 мм рт. ст. Ответ дайте в километрах.
Найдите длину диагонали прямоугольника, вершины которого имеют координаты (3;1), (11;1), (11;16), (3;16).
В кафе на одной полке в случайном порядке стоят 50 чайных чашек: 30 зеленых, 10 красных и 10 синих. На другой полке в случайном порядке стоят 50 блюдец: 30 зеленых, 10 красных и 10 синих. Найдите вероятность того, что случайно выбранная чашка и блюдце будут зелëного цвета.
Найдите корень уравнения \(\sqrt{-x}=x+6\). Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Четырёхугольник ABCD вписан в окружность. Угол BAD равен 127°. Найдите угол BCD. Ответ дайте в градусах.
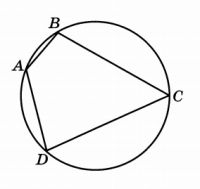
На рисунке изображён график функции \(y=f(x)\). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой \(-4.\) Найдите значение производной функции в точке \(x_0=-4.\)
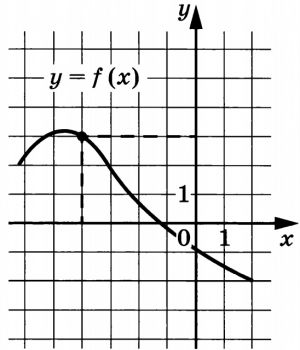
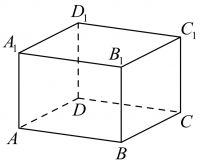
В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ известно, что AB=9, BC=8, AA₁=6. Найдите объём многогранника, вершинами которого являются точки A, B, C, B₁.
Найдите значение выражения \(\cos\alpha\), если \(\mathrm{tg\,} \alpha=\dfrac{\sqrt{91}}{3}\) и \(\alpha\in\bigg(\pi;\dfrac{3\pi}{2}\bigg)\).
Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с фокусным расстоянием \(f = 60 \,см\). Расстояние \(d_1\) от линзы до лампочки может изменяться в пределах от 95 см до 115 см а расстояние \(d_2\) от линзы до экрана - в пределах от 140 см до 160 см. Изображение на экране будет чётким, если выполнено соотношение \(\dfrac1{d_1}+\dfrac1{d_2}=\dfrac1{f}\). На каком наименьшем расстоянии от линзы нужно поместить лампочку, чтобы её изображение на экране было чётким? Ответ дайте в сантиметрах.
Первый и второй насосы наполняют бассейн за 35 минут, второй и третий - за 40 минут, а первый и третий - за 56 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Найдите наибольшее значение функции \(y=(x-6)e^{7-x}\) на отрезке \([2;15]\).
а) Решите уравнение \(\sin^2\left(\dfrac{x}{4}+\dfrac{\pi}{4}\right)\sin^2\left(\dfrac{x}{4}-\dfrac{\pi}{4}\right)=0,375\sin^2\left(-\dfrac{\pi}{4}\right)\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([-3\pi;\pi]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -3π | 18. -8π/3 | 19. -7π/3 | 20. -2π |
| 21. -5π/3 | 22. -4π/3 | 23. -π | 24. -2π/3 |
| 25. -π/3 | 26. 0 | 27. π/3 | 28. 2π/3 |
| 29. π |
В правильной шестиугольной призме \(ABCDEFA_1B_1C_1D_1E_1F_1\) сторона основания \(AB\) равна 6, а боковое ребро \(AA_1\) равно \(5\sqrt3\). На ребре \(DD_1\) отмечена точка \(M\) так, что \(DM:MD_1=2:3\). Плоскость \(\alpha\) параллельна прямой \(A_1F_1\) и проходит через точки \(M\) и \(B\).
а) Докажите, что сечение призмы \(ABCDEFA_1B_1C_1D_1E_1F_1\) плоскостью \(\alpha\) - равнобедренная трапеция.
б) Найдите объём пирамиды, вершиной которой является точка \(A_1\), а основанием - сечение призмы \(ABCDEFA_1B_1C_1D_1E_1F_1\) плоскостью \(\alpha\).
Решите неравенство \(\left(5\cdot 0{,}2^{x+0{,}5}-0{,}2\cdot5^{x+0{,}5}\right)\left(0{,}5\log^2_{0{,}2}(x+0{,}5)-2\log_5(x+0{,}5)\right)>0\)
В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 22,5°. Точка P лежит вне прямоугольника, а угол BPC равен 135°.
а) Докажите, что углы BCP и POB равны.
б) Прямая PO пересекает сторону AD в точке F. Найдите DF, если BP=7 и CP=5√2.
15 января планируется взять кредит в банке на 3 года. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что за 24-й месяц кредитования нужно выплатить 45,2 тыс. рублей.
Сколько рублей нужно будет вернуть банку в течение всего срока кредитования?
Найдите все значения \(a\), при каждом из которых среди корней уравнения \(x^2-10x+35=a|x-6|\) будет ровно два положительных.
У Коли в копилке есть 2-рублёвые, 5-рублёвые и 10-рублёвые монеты. Если взять 20 монет, то среди них обязательно найдётся хотя бы одна 2-рублёвая. Если взять 25 монет, то среди них обязательно найдётся хотя бы одна 5-рублёвая. Если взять 30 монет, то среди них обязательно найдётся хотя бы одна 10-рублёвая.
а) Может ли у Коли быть 50 монет?
б) Какое наибольшее количество монет может быть у Коли?
в) Какая наибольшая сумма рублей может быть у Коли?
Введите ответ в форме строки "да;123;1234". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.