36 вариантов ЕГЭ 2021
Меню курса
20 вариант ЕГЭ Ященко с решением
Задачу №1 правильно решили 24 840 человек, что составляет 72% от выпускников города. Сколько всего выпускников в этом городе?
На рисунке показан курс индийской рупии, установленный Центробанком на все рабочие дни марта 2019 года. По горизонтали указаны числа месяца, по вертикали — цена 100 индийских рупий в рублях. Для наглядности точки соединены отрезками.
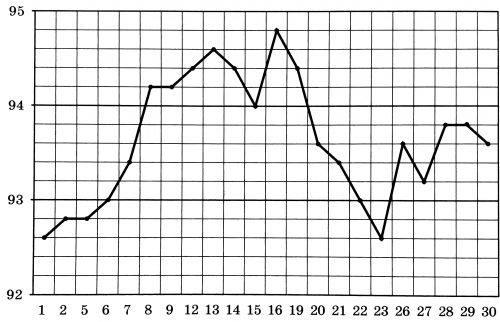
Определите, сколько рабочих дней в период с 16 по 30 марта 2019 года стоимость 100 индийских рупий была ниже 94 рублей.
Найдите площадь треугольника, изображённого на рисунке.
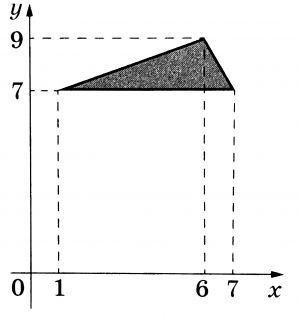
В коробке 8 чёрных и 5 белых шаров. Случайным образом достают 6 шаров. Во сколько раз событие «среди выбранных шаров ровно четыре чёрных» более вероятно, чем событие «среди выбранных шаров ровно пять чёрных»?
Найдите корень уравнения \(\log_{7}{(x+18)}=2\log_{7}{(2-x)}\).Если уравнение имеет более одного корня, в ответе запишите наибольший из корней.
Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 9. Найдите среднюю линию этой трапеции.
На рисунке изображён график функции \(y=F(x)\) одной из первообразных функции \(f(x)\), определённой на интервале (-3;6). Найдите количество решений уравнения \(f(x)=0\) на отрезке [-2; 5].
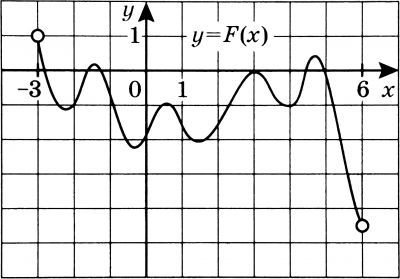
Шар вписан в цилиндр. Площадь поверхности шара равна 74. Найдите площадь полной поверхности цилиндра.
Найдите значение выражения \(2{,}5^{\frac{1}{7}}\cdot2^{\frac{2}{7}}\cdot10^{\frac{6}{7}}\)
Два тела, массой \(m=10\) кг каждое, движутся с одинаковой скоростью \(v=10\) м/с под углом \(2\alpha\) друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле \(Q=mv^2\sin^2{\alpha}\), где \(m\) - масса в килограммах, \(v\) - скорость в м/с. Найдите, под каким наименьшим углом \(2\alpha\) (в градусах) должны двигаться тела, чтобы в результате соударения выделилось энергии не менее 750 джоулей.
Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 6 рабочих, во второй 15 рабочих. Через 5 дней после начала работы в первую бригаду перешли 7 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.
Найдите наименьшее значение функции \(y=4x^2-12x+4\ln{x}-10\) на отрезке \(\left[\dfrac{12}{13};\dfrac{14}{13}\right]\)
а) Решите уравнение \(125^{\sin^2{x}}=(\sqrt{5})^{5\sin{2x}}\cdot0{,}2\)
б) Найдите все корни этого уравнения, принадлежащие промежутку \([-3\pi;-2\pi]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. \(\pi n,\; n\in\mathbb{Z}\) | 2. \(\dfrac{\pi}{6}+\pi n,\; n\in\mathbb{Z}\) | 3. \(\dfrac{\pi}{4}+\pi n,\; n\in\mathbb{Z}\) | 4. \(\dfrac{\pi}{3}+\pi n,\; n\in\mathbb{Z}\) |
| 5. \(\dfrac{\pi}{2}+\pi n,\; n\in\mathbb{Z}\) | 6. \(\dfrac{2\pi}{3}+\pi n,\; n\in\mathbb{Z}\) | 7. \(\dfrac{3\pi}{4}+\pi n,\; n\in\mathbb{Z}\) | 8. \(\dfrac{5\pi}{6}+\pi n,\; n\in\mathbb{Z}\) |
| 9. \(\mathrm{arctg\,}\dfrac15+\pi n,\; n\in\mathbb{Z}\) | 10. \(\mathrm{arctg\,}\dfrac14+\pi n,\; n\in\mathbb{Z}\) | 11. \(\mathrm{arctg\,}\dfrac13+\pi n,\; n\in\mathbb{Z}\) | 12. \(\mathrm{arctg\,}\dfrac12+\pi n,\; n\in\mathbb{Z}\) |
| 13. \(-\mathrm{arctg\,}\dfrac15+\pi n,\; n\in\mathbb{Z}\) | 14. \(-\mathrm{arctg\,}\dfrac14+\pi n,\; n\in\mathbb{Z}\) | 15. \(-\mathrm{arctg\,}\dfrac13+\pi n,\; n\in\mathbb{Z}\) | 16. \(-\mathrm{arctg\,}\dfrac12+\pi n,\; n\in\mathbb{Z}\) |
б)
| 17. \(-3\pi\) | 18. \(-\dfrac{17\pi}{6}\) | 19. \(-\dfrac{11\pi}{4}\) | 20. \(-\dfrac{8\pi}{3}\) |
| 21. \(-\dfrac{6\pi}{2}\) | 22. \(-\dfrac{7\pi}{3}\) | 23. \(-\dfrac{9\pi}{4}\) | 24. \(-\dfrac{13\pi}{6}\) |
| 25. \(-2\pi\) | 26. \(\mathrm{arctg\,}\dfrac15-3\pi\) | 27. \(\mathrm{arctg\,}\dfrac14-3\pi\) | 28.\(\mathrm{arctg\,}\dfrac13-3\pi\) |
| 29.\(\mathrm{arctg\,}\dfrac12-3\pi\) | 30. \(-\mathrm{arctg\,}\dfrac15-2\pi\) | 31. \(-\mathrm{arctg\,}\dfrac14-2\pi\) | 32. \(-\mathrm{arctg\,}\dfrac13-2\pi\) |
| 33. \(-\mathrm{arctg\,}\dfrac12-2\pi\) |
Основание пирамиды SABC - равносторонний треугольник ABC. Боковое ребро SA перпендикулярно плоскости основания, точки М и N - середины рёбер BC и AB соответственно, причём SN=AM.
а) Докажите, что угол между прямыми AM и SN равен 60°.
б) Найдите расстояние между этими прямыми, если BC=6.
Решите неравенство \(\log_{\frac{1}{4}}{(5-5x)}\leqslant\log_{\frac{1}{4}}{(x^2-3x+2)}+\log_{4}{(x+4)}\)
В треугольнике АВС все стороны различны. Прямая, содержащая высоту ВН треугольника АВС, вторично пересекает описанную около этого треугольника окружность в точке K. Отрезок BN-диаметр этой окружности.
а) Докажите, что AC и KN параллельны.
б) Найдите расстояние от точки N до прямой AC, если радиус описанной около треугольника ABC окружности равен 6√6, ∠BAC=30°, ∠ABC=105°
По бизнес-плану четырёхлетний проект предполагает начальное вложение — 10 млн рублей. По итогам каждого года планируется прирост вложенных средств на 12 % по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: целое число n млн рублей и в первый, и во второй годы, а также целое число m млн рублей и в третий, и в четвёртый годы. Найдите наименьшее значение n, при котором первоначальные вложения за два года вырастут как минимум в полтора раза, и наименьшее значение m, такое, что при найденном ранее значении n первоначальные вложения за четыре года как минимум утроятся.
Запишите значения n и m через точку с запятой без пробелов.
Найдите все значения \(a\), при каждом из которых система уравнений \(\begin{cases}y=(a+2)x^2+2ax+a-2\\y^2=x^2\end{cases}\)имеет ровно четыре различных решения.
Сторона квадрата на 2 см длиннее ширины прямоугольника, площади этих фигур равны, а все стороны – целые числа.
а) Может ли ширина прямоугольника быть равной 6?
б) Может ли длина прямоугольника быть равной 9?
в) Найдите все возможные варианты таких пар прямоугольников и квадратов.
Введите ответ в форме строки "да;да;1;2;3;4". Где ответы на пункты разделены ";", первые два ответа с маленькой буквы, а в пункте В перечислите возможные длины стороны квадрата по возрастанию через точку с запятой.