7 вариант ЕГЭ Ященко с решением

Стоимость проездного билета на месяц составляет 1450 рублей, а стоимость билета на одну поездку - 46 рублей. Ира купила проездной и сделала за месяц 48 поездок. На сколько рублей больше она бы потратила, если бы покупала билеты на одну поездку?

В ходе химической реакции масса исходного вещества (реагента), которое ещё не вступило в реакцию, постепенно уменьшается. На графике показана зависимость массы реагента от времени. На горизонтальной оси отмечено время, прошедшее с начала реакции, в минутах, на вертикальной оси - масса реагента, который ещё не вступил в реакцию, в граммах. Определите по графику, сколько граммов реагента останется через 1 минуту после начала реакции.

​

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

​

Научная конференция проводится в 4 дня. Всего запланировано 50 докладов: первые два дня по 13 докладов, остальные распределены поровну между третьим и четвёртым днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции?

Найдите корень уравнения \(\bigg(\dfrac1{4}\bigg)^{x-2{,}5}=\dfrac1{8}\)

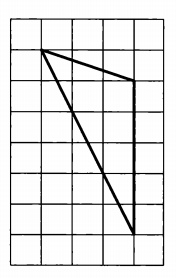
Градусная мера дуги AB окружности, не содержащей точку D, равна 106°. Градусная мера дуги DE окружности, не содержащей точку A, равна 48°. Найдите угол ACB. Ответ дайте в градусах.

​

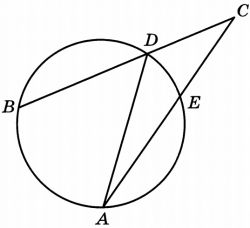
На рисунке изображён график \(y=f'(x)\) - производной функции \(f(x)\). На оси абсцисс отмечены 10 точек: \(x_1\), \(x_2\), \(x_3\), \(x_4\), \(x_5\), \(x_6\), \(x_7\), \(x_8\), \(x_9\), \(x_{10}\). Сколько из этих точек лежит на промежутках убывания функции \(f(x)\)?

​

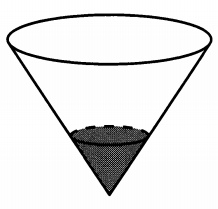
В сосуде, имеющем форму конуса, уровень жидкости достигает 0,25 высоты. Объём жидкости равен 5 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

​

Найдите значение выражения \(4\cos4\alpha\), если \(\sin2\alpha=-0{,}4\).

Независимое агентство намерено ввести рейтинг \(R\) новостных изданий на основе показателей информативности \(In\), оперативности \(Op\) и объективности \(Tr\) публикаций. Каждый отдельный показатель - целое число от -1 до 1. Составители рейтинга считают, что информативность публикаций ценится вчетверо, а объективность - вдвое дороже, чем оперативность, то есть \(R=\dfrac{4In+Op+2Tr}{A}\). Найдите, каким должно быть число \(A\), чтобы издание, у которого все показатели максимальны, получило рейтинг 1.

Из пункта А в пункт В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 63 км/ч, а вторую половину пути - со скоростью, большей скорости первого на 22 км/ч, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.

Найдите точку минимума функции \(y=11x-\ln(x+4)^{11}-3\).

а) Решите уравнение \(\sin\bigg(2x+\dfrac{2\pi}{3}\bigg)\cos\bigg(4x+\dfrac{\pi}{3}\bigg)-\cos2x=\dfrac{\sin^2x}{\cos\left(-\dfrac{\pi}{3}\right)}\)
​б) Найдите все корни этого уравнения, принадлежащие отрезку \(\bigg[-2\pi;\dfrac{3\pi}{2}\bigg]\).

В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ сторона основания AB равна 2√3, а боковое ребро AA₁ равно 3. На рёбрах A₁D₁ и DD₁ отмечены соответственно точки K и M так, что A₁K=KD₁, а DM:MD₁=2:1.
а) Докажите, что прямые MK и BK перпендикулярны.
б) Найдите угол между плоскостями BMK и BCC₁. Ответ дайте в градусах.

Решите неравенство \(\dfrac{6\cdot5^x-11}{25^{x+0,5}-6\cdot5^x+1}\geqslant0{,}25\)

На сторонах AC, AB и BC прямоугольного треугольника ABC с прямым углом C вне треугольника ABC построены равнобедренные прямоугольные треугольники AKC, ALB и BMC с прямыми углами K, L и M соответственно.
а) Докажите, что LC – высота треугольника KLM.
б) Найдите площадь треугольника KLM, если LC=4.

Александр хочет купить пакет акций быстрорастущей компании. В начале года у Александра не было денег на покупку акций, а пакет стоит 100 000 рублей. В середине каждого месяца Александр откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 30%. Какую наименьшую сумму нужно откладывать Александру каждый месяц, чтобы через некоторое время купить желаемый пакет акций?

Найдите, при каких неотрицательных значениях \(a\) функция \(f(x)=3ax^4-8x^3+3x^2-7\) на отрезке \([-1;1]\) имеет ровно одну точку минимума.

Для каждого натурального числа n обозначим через n! произведение первых n натуральных чисел (1! = 1).