36 вариантов ЕГЭ 2021
Меню курса
16 вариант ЕГЭ Ященко с решением
Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 60 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?
На диаграмме показана цена палладия во все месяцы 2017 и 2018 годов. По горизонтали указаны месяцы, по вертикали — цена тройской унции палладия в долларах США. Для наглядности точки соединены отрезками. Определите наименьшую цену в долларах США тройской унции палладия в первом полугодии 2018 года.

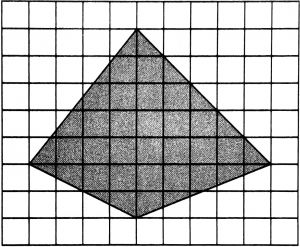
На клетчатой бумаге с размером клетки \(1\times1\)изображён четырёхугольник. Найдите его площадь.
На заводе выпускают насосы для колодцев, из них 3% выходят со сборочной линии со скрытым дефектом. При контроле качества продукции выявляется 90% дефектных насосов. Остальные насосы поступают в продажу. Найдите вероятность того, что произведённый насос окажется в продаже.
Найдите корень уравнения \(\log_{5}{(x+7)}=\log_{5}(5-x)-1\).
Острые углы прямоугольного треугольника равны 80° и 10°. Найдите угол между биссектрисой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Прямая \(y=6x+7\) параллельна касательной к графику функции \(y=x^2-5x+6\). Найдите абсциссу точки касания.
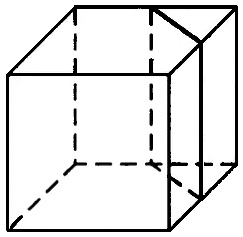
Объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины, равен 11. Найдите объём куба.
Найдите значение выражения \(\dfrac{20}{(2\sqrt{2})^2}\).
При адиабатическом процессе для идеального газа выполняется закон \(pV^k=7{,}776\cdot10^6\,Па\cdotм^4\), где \(p\) – давление в газе в паскалях, \(V\) – объём газа в кубических метрах, \(k=\dfrac{4}{3}\). Найдите, какой объём \(V\) (в куб. м) будет занимать газ при давлении \(p\), равном \(3,75\cdot10^6\,Па\)
Теплоход, скорость которого в неподвижной воде равна 16 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 2 км/ч, стоянка длится 5 часов, а в исходный пункт теплоход возвращается через 53 часа после отплытия из него. Сколько километров прошёл теплоход за весь рейс?
Найдите точку минимума функции \(y=-\dfrac{x}{x^2+900}\).
а) Решите уравнение \(4\sin^4x+7\cos^2x-4=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([-5\pi; -4\pi]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -5π | 18. -29π/6 | 19. -19π/4 | 20. -14π/3 |
| 21. -9π/2 | 22. -13π/3 | 23. -17π/4 | 24. -25π/6 |
| 25. -4π | 26. -23π/6 | 27. -15π/4 | 28. -11π/3 |
| 29. -7π/2 |
Основанием пирамиды FABC является правильный треугольник ABC со стороной 48. Все боковые рёбра пирамиды равны 40. На рёбрах FB и FC отмечены соответственно точки K и N так, что FK=FN=10. Через точки K и N проведена плоскость α, перпендикулярная плоскости ABC.
а) Докажите, что плоскость α делит медиану AM в отношении 1:3.
б) Найдите расстояние от точки C до плоскости α.
Решите неравенство \(3\log^2_{4}{(4-x)^8}+4\log_{0{,}5}{(4-x)^6}\geqslant72\)
В треугольнике \(ABC\) известно, что \(AC=26\) и \(AB=BC=38\).
а) Докажите, что средняя линия треугольника, параллельная стороне \(AC\), пересекает окружность, вписанную в треугольник \(ABC\).
б) Найдите отношение длин отрезков, на которые окружность делит среднюю линию, параллельную стороне \(AC\).
15 декабря планируется взять кредит в банке на сумму 1 000 000 рублей на (n+1) месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца с 1-го по n-й долг должен быть на 40 тысяч рублей меньше долга на 15-е число предыдущего месяца;
- 15-го числа n-го месяца долг составит 200 тысяч рублей;
- к 15-му числу (n+1)-го месяца кредит должен быть полностью погашен.
Найдите r, если известно, что общая сумма выплат после полного погашения кредита составит 1 378 тысяч рублей.
Найдите все значения параметра \(a\), при каждом из которых любое значение из промежутка \([-1{,}5;-0{,}5]\) является решением неравенства \((4|x|-a-3)(x^2-2x-2-a)\geqslant0\).
Группу детей можно перевезти автобусами модели А или автобусами модели Б. Известно, что в автобусе модели А количество мест больше 40, но меньше 50, а в автобусах модели Б — больше 50, но меньше 60. Если всех детей рассадить в автобусы модели А, то все места будут заняты. Если всех детей рассадить в автобусы модели Б, то все места также будут заняты, но потребуется на один автобус меньше.
а) Может ли потребоваться 4 автобуса модели Б?
б) Найдите наибольшее возможное количество детей в группе, если известно, что их меньше 300.
в) Найдите наибольшее возможное количество автобусов модели А.
Введите ответ в форме строки "да;123;1234". Где ответы на пункты разделены ";", и первый ответ с маленькой буквы.