36 вариантов ЕГЭ 2021
Меню курса
19 вариант ЕГЭ Ященко с решением
На счету Юлиного мобильного телефона было 93 рубля, а после разговора с Мишей осталось 28 рублей. Сколько минут длился разговор с Мишей, если одна минута разговора стоит 2 рубля 50 копеек?
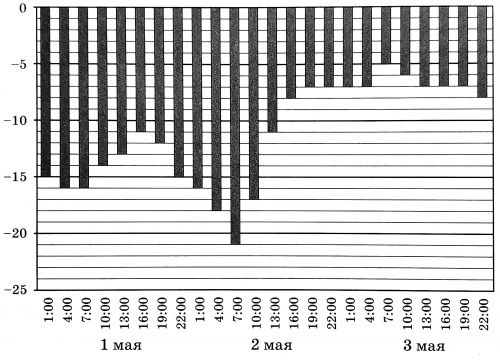
На диаграмме показаны значения температуры в Норильске с 1 по 3 мая 2019 года. По горизонтали указаны моменты измерений, по вертикали - температура в градусах Цельсия. Определите по диаграмме значение наибольшей температуры в Норильске 1 мая.
Точки O(0; 0), A(23; 0), B(20; 18), C(3; 18) являются вершинами трапеции. Найдите длину её средней линии.
Вероятность того, что новый фен прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,88. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Найдите корень уравнения \(\log_{2}{(8-x)}=2\log_{2}{(4+x)}\). Если уравнение имеет более одного корня, в ответе запишите наименьший из корней.
В треугольнике со сторонами 8 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой из этих сторон, равна 1. Чему равна высота, проведённая ко второй стороне?
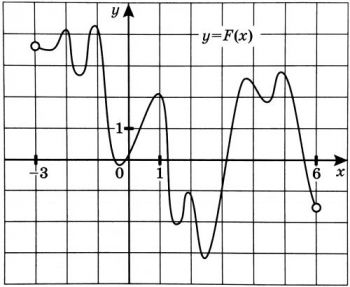
На рисунке изображён график функции \(y=F(x)\) - одной из первообразных функции \(f(x)\) определённой на интервале \((-3; 6)\). Найдите количество решений уравнения \(f(x)=0\) на отрезке \([-2; 5]\).
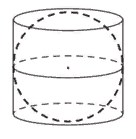
Шар, объём которого равен 64, вписан в цилиндр. Найдите объём цилиндра.
Найдите значение выражения \(\dfrac{\left(2^{\frac{4}{7}}\cdot3^{\frac{2}{3}}\right)^{21}}{6^{12}}\).
Груз массой \(0{,}3\) кг колеблется на пружине. Его скорость \(v\) меняется по закону \(v=v_0\cos\dfrac{2\pi t}{T}\), где \(t\) - время с момента начала колебаний, \(Т=2\) с - период колебаний, \(v_0=0{,}2\) м/с. Кинетическая энергия \(E\) (в джоулях) груза вычисляется по формуле \(E=\dfrac{mv^2}{2}\), где \(m\) - масса груза в килограммах, \(v\) - скорость груза в м/с. Найдите кинетическую энергию груза через 33 с после начала колебаний. Ответ дайте в джоулях.
На изготовление 33 деталей первый рабочий тратит на 8 часов меньше, чем второй рабочий на изготовление 77 таких же деталей. Известно, что первый рабочий за час делает на 4 детали больше, чем второй. Сколько деталей за час делает второй рабочий?
Найдите наименьшее значение функции \(y=2x^2-5x+\ln x-5\) на отрезке \(\left[\dfrac{5}{6};\dfrac{7}{6}\right]\).
а) Решите уравнение \(8^{\cos^2{x}}=\left(\sqrt{2}\right)^{5\sin{2x}}\cdot0{,}5\)
б) Найдите все корни этого уравнения, принадлежащие промежутку \(\left[\dfrac{5\pi}{2};4\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. \(\pi n,\; n\in\mathbb{Z}\) | 2. \(\dfrac{\pi}{6}+\pi n,\; n\in\mathbb{Z}\) | 3. \(\dfrac{\pi}{4}+\pi n,\; n\in\mathbb{Z}\) | 4. \(\dfrac{\pi}{3}+\pi n,\; n\in\mathbb{Z}\) |
| 5. \(\dfrac{\pi}{2}+\pi n,\; n\in\mathbb{Z}\) | 6. \(\dfrac{2\pi}{3}+\pi n,\; n\in\mathbb{Z}\) | 7. \(\dfrac{3\pi}{4}+\pi n,\; n\in\mathbb{Z}\) | 8. \(\dfrac{5\pi}{6}+\pi n,\; n\in\mathbb{Z}\) |
| 9. \(\mathrm{arctg\,}2+\pi n,\; n\in\mathbb{Z}\) | 10. \(\mathrm{arctg\,}3+\pi n,\; n\in\mathbb{Z}\) | 11. \(\mathrm{arctg\,}4+\pi n,\; n\in\mathbb{Z}\) | 12. \(\mathrm{arctg\,}5+\pi n,\; n\in\mathbb{Z}\) |
| 13. \(-\mathrm{arctg\,}2+\pi n,\; n\in\mathbb{Z}\) | 14. \(-\mathrm{arctg\,}3+\pi n,\; n\in\mathbb{Z}\) | 15. \(-\mathrm{arctg\,}4+\pi n,\; n\in\mathbb{Z}\) | 16. \(-\mathrm{arctg\,}5+\pi n,\; n\in\mathbb{Z}\) |
б)
| 17. \(\dfrac{5\pi}{2}\) | 18. \(\dfrac{8\pi}{3}\) | 19. \(\dfrac{11\pi}{4}\) | 20. \(\dfrac{17\pi}{6}\) |
| 21. \(3\pi\) | 22. \(\dfrac{19\pi}{6}\) | 23. \(\dfrac{13\pi}{4}\) | 24. \(\dfrac{10\pi}{3}\) |
| 25. \(\dfrac{7\pi}{2}\) | 26. \(\dfrac{11\pi}{3}\) | 27. \(\dfrac{15\pi}{4}\) | 28. \(\dfrac{23\pi}{6}\) |
| 29. \(4\pi\) | 30. \(\mathrm{arctg\,}2+3\pi\) | 31. \(\mathrm{arctg\,}3+3\pi\) | 32. \(\mathrm{arctg\,}4+3\pi\) |
| 33. \(-\mathrm{arctg\,}2+4\pi\) | 34. \(-\mathrm{arctg\,}3+4\pi\) | 35. \(-\mathrm{arctg\,}4+4\pi\) |
Основание пирамиды \(SABC\) – равносторонний треугольник \(ABC\). Боковое ребро \(SA\) перпендикулярно плоскости основания, точки \(M\) и \(N\) - середины рёбер \(BC\) и \(AB\) соответственно, причём \(SN=AM\).
а) Докажите, что угол между прямыми \(AM\) и \(SN\) равен \(60°\).
б) Найдите расстояние между этими прямыми, если \(BC=3\sqrt{2}\).
Решите неравенство \(4^{2x+1{,}5}-9^{x+0{,}5}\geqslant2\cdot12^x\)
В треугольнике ABC все стороны различны. Прямая, содержащая высоту BH треугольника ABC, вторично пересекает описанную около этого треугольника окружность в точке F. Отрезок BD - диаметр этой окружности.
а) Докажите, что AD=CF.
б) Найдите DF, если радиус описанной около треугольника ABC окружности равен 12, угол BAC=35°, угол ACB=65°.
В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
- каждый январь долг возрастает на 14% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга, равную 3,249 млн рублей.
Сколько миллионов рублей было взято в банке, если известно, что он был полностью погашен двумя равными платежами (то есть за два года)?
Найдите все значения \(a\), при каждом из которых уравнение \(\dfrac{x^2+x+a}{x^2-2x+a^2+6a}=0\) имеет ровно два различных корня.
Сторона квадрата на 3 см длиннее ширины прямоугольника, площади этих фигур равны, а все стороны – целые числа.
а) Может ли ширина прямоугольника быть равной 8?
б) Может ли длина прямоугольника быть равной 16?
в) Найдите все возможные варианты таких пар прямоугольников и квадратов.
Введите ответ в форме строки "да;да;1;2;3;4". Где ответы на пункты разделены ";", первые два ответа с маленькой буквы, а в пункте В перечислите возможные длины стороны квадрата по возрастанию через точку с запятой.