36 вариантов ЕГЭ 2026
1 вариант ЕГЭ Ященко 2026
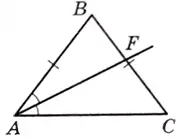
В равнобедренном треугольнике ABC с основанием AC провели биссектрису AF. Найдите угол AFC, если угол ABC равен 76°. Ответ дайте в градусах.
Даны векторы \(\vec{a}(-3;2)\) и \(\vec{b}(-1;-9)\). Найдите длину вектора \(3\vec{a}-2\vec{b}\)
Дано два цилиндра. Объём первого цилиндра равен 102. У второго цилиндра высота в 3 раза больше, а радиус основания в 2 раза меньше, чем у первого. Найдите объём второго цилиндра.

Фабрика выпускает сумки. В среднем 6 сумок из 250 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе останется в обоих автоматах, равна 0,55. Найдите вероятность того, что к концу дня кофе закончится в обоих автоматах.
Найдите корень уравнения \(\sqrt{15x}=1\frac23x\). Если уравнение имеет больше одного корня, в ответе запишите больший из корней.
Найдите \(\log_a\dfrac{a^4}{b^5}\), если \(\log_ab=15\)
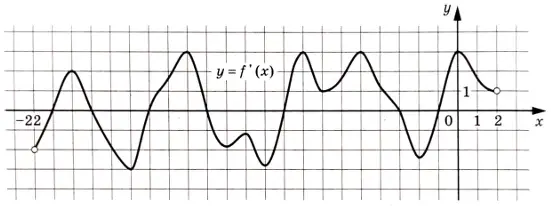
На рисунке изображён график \(y=f'(x)\) — производной функции \(f(x)\), определённой на интервале \((-22;2)\). Найдите количество точек максимума функции \(f(x)\), принадлежащих отрезку \([-18;1]\)
В ходе распада радиоактивного изотопа его масса уменьшается по закону \( m=m_0\cdot2^{-\frac{t}{T}} \), где \( m_0 \) — начальная масса изотопа, \( t \) — время, прошедшее от начального момента, \( T \) — период полураспада. В начальный момент времени масса изотопа 192 мг. Период его полураспада составляет 10 минут. Найдите, через сколько минут масса изотопа будет равна 6 мг.
Катер, скорость которого в неподвижной воде равна 28 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 2 км/ч, стоянка длится 4 часа, а в исходный пункт катер возвращается через 18 часов после отплытия из него. Сколько километров прошёл катер за весь рейс?
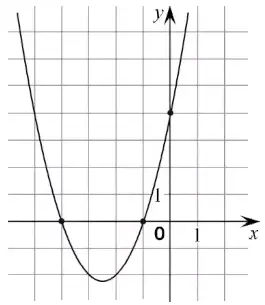
На рисунке изображен график функции \(f(x)=ax^2+bx+c\). Найдите \(f(3)\)
Найдите точку максимума функции \(y=x^2+12\ln(x+5)-7\)
а) Решите уравнение \(\sqrt{2\cos^3x-\sin^2x-2\cos x-\sin x}=\sqrt{\cos\left(\frac{\pi}2+x\right)}\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-4\pi;-\dfrac{5\pi}2\right]\)
Запишите номера всех верных ответов на пункты а) и б) по возрастанию, через запятую, без пробелов. В первое поле на пункт а), во второе - на пункт б)
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -4π | 18. -23π/6 | 19. -15π/4 | 20. -11π/3 |
| 21. -7π/2 | 22. -10π/3 | 23. -13π/4 | 24. -19π/6 |
| 25. -3π | 26. -17π/6 | 27. -11π/4 | 28. -8π/3 |
| 29. -5π/2 |
В пирамиде SABCD с высотой SA основанием является квадрат ABCD, точка K — середина ребра SB. Прямая DK пересекается с плоскостью SAC в точке N.
a) Докажите, что прямая a, проходящая через точку N параллельно прямой SC, делит диагональ основания AC в отношении 1:2.
б) Найдите угол между прямыми DK и SC, если AB=2√3, SA=6.
Решите неравенство \(\dfrac{9^x-3^{x+2}+8}{\log_{\frac16}^2 (5^x-2)+\log_{\frac16}{(5^x-2)}^2+1}\leqslant0\)
В июне 2028 года Пётр Иванович планирует взять кредит в банке на 5 лет в размере целого числа миллионов рублей. Условия его возврата таковы:
- в январе каждого года долг увеличивается на 20% от суммы долга на конец предыдущего года;
- в период с февраля по июнь в каждый из 2029, 2030 и 2031 годов необходимо выплатить только проценты по кредиту, начисленные в январе соответствующего года;
- в период с февраля по июнь в каждый из 2032 и 2033 годов платежи по кредиту равные, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наибольший размер кредита, при котором общая сумма выплат по кредиту не превысит 10 млн рублей.
В прямоугольную трапецию ABCD с большим основанием CD и прямыми углами A и D вписана окружность с центром в точке O радиуса R. Точка G — точка касания данной окружности и стороны AB трапеции ABCD. Биссектриса угла ADC перпендикулярна стороне BC и пересекает её в точке N.
a) Докажите, что BN=(√2-1)R.
б) Найдите радиус окружности, вписанной в четырёхугольник BNOG, если R=6.
Найдите все значения \(a\), при каждом из которых система уравнений \(
\begin{cases}
\left(|x|-a^2\right)^2+(y-4a)(y+4a)=9a^2-2y-1\\
y+1=6\sqrt{a}
\end{cases}
\) имеет ровно два различных решения.
У Ивана Ильича есть коллекция монет. Если все его монеты разложить в одинаковые большие классеры*, то потребуется k классеров, причём 5 ячеек в одном классере останутся пустыми. Если же их разложить в одинаковые маленькие классеры, то потребуется k+2 классеров и также 5 ячеек в одном классере останутся пустыми. Известно, что в большом классере больше 150, но меньше 160 ячеек, а в маленьком — больше 100, но меньше 120 ячеек.
*Классер — альбом (папка) для коллекционирования марок, монет.