6 вариант ЕГЭ Ященко 2026

В треугольнике ABC высота AH равна 4√6, AB=BC, AC=25. Найдите косинус угла CAB.

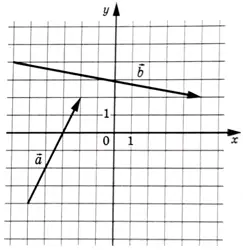
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\), координаты у которых — целые числа. Найдите \(\cos\angle(\vec{a};\vec{b})\)

Прямоугольный параллелепипед описан около сферы радиуса 3. Найдите площадь его поверхности.

В магазине в одной коробке лежат вперемешку ручки с чёрными, синими и красными чернилами, одинаковые на вид. Покупатель случайным образом выбирает одну ручку. Вероятность того, что она окажется синей или чёрной, равна 0,86, а того, что она окажется красной или синей, равна 0,58. Найдите вероятность того, что ручка окажется синей.

Правильный игральный кубик бросили десять раз. Известно, что в какой-то момент сумма выпавших при бросаниях очков оказалась равна 3. Какова вероятность того, что к этому моменту был сделан ровно один бросок? Ответ округлите до сотых.

Найдите корень уравнения \(2^{-7-4x}=64^x\)

Найдите значение выражения \(2^{3+\log_212}\)

Материальная точка движется прямолинейно по закону \(x(t)=\frac12t^4-t^3+3t^2+7t\), где \(x\) — расстояние от точки отсчёта в метрах, \(t\) — время в секундах, прошедшее с начала движения. Найдите её скорость (в метрах в секунду) в момент времени \(t=2\)с.

Груз массой 0,58 кг колеблется на пружине. Его скорость \( v \) меняется по закону \( v = v_0 \sin \dfrac{2\pi t}{T} \), где \( t \) — время с момента начала колебаний, \( T = 6\)с — период колебаний, \( v_0 = 2\)м/с. Кинетическая энергия \( E \) (в джоулях) груза вычисляется по формуле \( E = \dfrac{mv^2}{2} \), где \( m \) — масса груза в килограммах, \( v \) — скорость груза в м/с. Найдите кинетическую энергию груза через 4 секунды после начала колебаний. Ответ дайте в джоулях.

Смешали 55-процентный и 30-процентный растворы кислоты и получили 40-процентный раствор кислоты. Если к полученному раствору добавить 10 кг чистой воды, то получится 32-процентный раствор кислоты. Сколько килограммов 55-процентного раствора использовали для получения смеси?

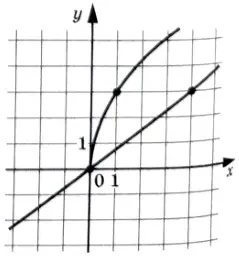
На рисунке изображены графики функций \( f(x) = kx + b \) и \( g(x) = p\sqrt{x} \), которые пересекаются в начале координат и в точке B. Найдите абсциссу точки B.

​

Найдите наименьшее значение функции \(y=2x^3+9x^2+12x-5\) на отрезке \([-3;4]\)

а) Решите уравнение \(\log_3^3{(x-3)}^2+8\log_3\dfrac1{(x-3)}+16=\log_3^2\dfrac1{{(x-3)}^4}\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \( \left[ \log_{0,6} \dfrac16;\log_{0,8}\dfrac18\right] \)

В правильной пирамиде SABCD с высотой SO точка K — середина ребра SB. Прямая DK пересекается с плоскостью SAC в точке N.
a) Докажите, что прямая a, проходящая через точку N параллельно прямой SC, делит ребро SA в отношении 1:2.
б) Найдите расстояние между прямыми DK и SC, если AB=2√3, SO=9.

Решите неравенство \(\dfrac{\sqrt{x+5}}{2^{x^2-6}-9\cdot2^{0,5x^2-4,5}+1}\geqslant0\)

15 января планируется взять кредит в банке на сумму 3 млн 600 тыс. рублей на 12 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца из первых шести месяцев действия кредита долг возрастает на r% по сравнению с концом предыдущего месяца;
- 1-го числа каждого месяца из последних шести месяцев действия кредита долг возрастает на 2% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
​Известно, что общая сумма выплат после полного погашения кредита составит 4 млн 153,5 тысячи рублей. Найдите r.

В равнобедренную трапецию ABCD с большим основанием AD вписаны две окружности так, что одна из них касается сторон AB, BC и AD, вторая — сторон BC, CD и AD, а сами они касаются друг друга внешним образом. Точка касания стороны CD с одной из окружностей радиуса r делит сторону CD в отношении 1:9.
a) Докажите, что r=0,3·CD.
б) Найдите радиус окружности, описанной около трапеции ABCD, если AB=20.

Найдите все положительные значения \( a \), при каждом из которых система уравнений \(
\begin{cases}
(x+a)^4-y^4-0{,}5a^2(x+a)^2+0{,}5a^2y^2=0\\
y=ax+\dfrac{a}{2}
\end{cases}
\) имеет ровно четыре различных решения.

В трёхзначном числе \(\overline{abc}\) (равно \(100a+10b+c\)) произведение его цифр \(abc\) не равно 0.