36 вариантов ЕГЭ 2026
9 вариант ЕГЭ Ященко 2026
В треугольнике ABC угол B равен 68°, биссектрисы углов BAC и ACB пересекаются в точке O. Найдите угол AOC. Ответ дайте в градусах.
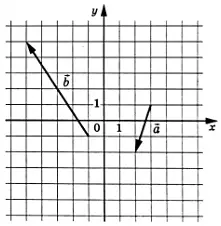
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\), координаты у которых — целые числа. Найдите длину вектора \(1{,}5\vec{b}-\vec{a}\)
Стороны основания правильной четырёхугольной пирамиды равны 6, боковые рёбра равны 5. Найдите площадь поверхности этой пирамиды.
На рок-фестивале выступают группы — по одной от каждого из участвующих городов, в том числе группы из Уфы, Москвы и Самары. Порядок выступления определяется жребием. Какова вероятность того, что группа из Самары будет выступать позже группы из Москвы, но раньше группы из Уфы? Ответ округлите до сотых.
Баскетболист на тренировке бросает мяч в кольцо 5 раз. Вероятность попадания при каждой отдельной попытке равна 0,8. Во сколько раз вероятность события «ровно 4 попадания» больше вероятности события «ровно 3 попадания»?
Найдите корень уравнения \(\sqrt{-x}=x+6\). Если уравнение имеет больше одного корня, в ответе запишите меньший из корней.
Найдите значение выражения \(\dfrac{6^{6,2}\cdot 5^{3,2}}{30^{4,2}}\)
Прямая \(y=-6x+15\) является касательной к графику функции \(y=x^3+5x^2-3x+6\). Найдите абсциссу точки касания.
Для обогрева помещения, температура в котором поддерживается на уровне \(T_п=15 °C\), через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды \(m=1{,}4\, кг/с\). Проходя по трубе расстояние \(x\), вода охлаждается от начальной температуры \(T_в=75 °C\) до температуры \(T\), причём \(x=\alpha\dfrac{cm}{γ}\log_{2}{\frac{T_в-T_п}{T-T_п}}\), где \(c=4200\,\dfrac{Вт\cdot с}{кг\cdot °C}\) - теплоёмкость воды, \(γ=63\,\dfrac{Вт}{м\cdot °C}\) - коэффициент теплообмена, а \(\alpha=1{,}8\) - постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 168 м.
Первый мастер изготавливает на 4 детали в час меньше, чем второй. Сколько деталей в час изготавливает второй мастер, если заказ на 220 деталей он выполняет на 2 часа 40 минут быстрее, чем первый мастер выполняет заказ на 260 деталей?
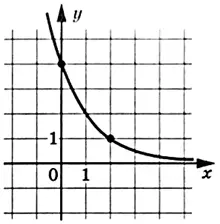
На рисунке изображён график функции \(f(x)=a^{x+b}\). Найдите \(f(-3)\)
Найдите точку минимума функции \(y=\dfrac{25x^2+169}{x}\)
а) Решите уравнение \( \cos2x\cdot\sin4x-\cos4x\cdot\sin\dfrac{5\pi}6=\cos\left(2x-\dfrac{\pi}2\right)\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([-3\pi;-2\pi]\)
Запишите номера всех верных ответов на пункты а) и б) по возрастанию, через запятую, без пробелов. В первое поле на пункт а), во второе - на пункт б)
а)
| 1. πn, n∈Z | 2. π/12+πn, n∈Z | 3. π/8+πn, n∈Z | 4. π/6+πn, n∈Z |
| 5. π/4+πn, n∈Z | 6. π/3+πn, n∈Z | 7. 3π/8+πn, n∈Z | 8. 5π/12+πn, n∈Z |
| 9. π/2+πn, n∈Z | 10. -π/12+πn, n∈Z | 11. -π/8+πn, n∈Z | 12. -π/6+πn, n∈Z |
| 13. -π/4+πn, n∈Z | 14. -π/3+πn, n∈Z | 15. -3π/8+πn, n∈Z | 16. -5π/12+πn, n∈Z |
б)
| 17. -3π | 18. -35π/12 | 19. -23π/8 | 20. -21π/8 |
| 21. -31π/12 | 22. -29π/12 | 23. -19π/8 | 24. -17π/8 |
| 25. -25π/12 | 26. -2π |
В правильной пирамиде SABCDEF высота SO в 3 раза больше стороны основания. На ребре SC отметили такую точку N, что треугольник BDN равносторонний.
а) Докажите, что точка N — середина ребра SC.
б) Найдите угол между плоскостями AFN и ABC.
Решите неравенство \( \dfrac{\log_{0,5}^{2}\left(x^4\right)-x^2}{100-x^2}\leqslant1\)
В январе 2028 года планируется открыть вклад на 4 года на целое число сотен тысяч рублей, а в январе 2029, 2030 и 2031 годов дополнительно вносить на этот вклад еще по 500 тысяч рублей. Банк в конце каждого года увеличивает сумму вклада на 10%. Какую наименьшую сумму надо вложить первоначально, чтобы банк начислил в качестве процентов более 1 млн рублей? Ответ дайте в рублях.
В треугольнике ABC со сторонами AB=6√5, AC=8√3 и BC=6 на стороне BC отметили точку D так, что BD:DC=1:2.
a) Докажите, что AD — высота треугольника ABC.
б) На луче BC отметили точку E такую, что AC — биссектриса треугольника BAE. Найдите радиус окружности, вписанной в треугольник BAE.
Найдите все значения \(a\), при каждом из которых система уравнений \(
\begin{cases}
(x-y)^2-(3a-8)^2+2(ax-ay+xy)=a^2-16\\
|xy|=a^2
\end{cases}
\) имеет не менее семи различных решений.
Коля записал на доске 20 различных натуральных чисел, каждое из которых меньше 1000. Петя записал на доске квадраты всех чисел, которые записал Коля. Получилось так, что среднее арифметическое любых трёх чисел, которые записал Петя, — целое число. Одно из чисел, записанных на доске, равно 625.