3 вариант ЕГЭ Ященко 2026

Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3:4, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 42.

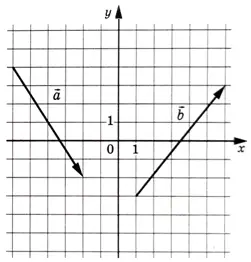
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\), координаты у которых — целые числа. Найдите скалярное произведение векторов \(\vec{a}\) и \(2\vec{b}\)

​

Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 5 раз, а образующая увеличится в 2 раза?

В чемпионате по шашкам участвует 76 спортсменов, среди которых 13 шашистов из России, в том числе Андрей Фомин. Для игр первого тура участников разбивают на игровые пары случайным образом. Найдите вероятность того, что в первом туре Андрей Фомин будет играть с каким-либо шашистом из России.

В группе туристов 16 человек, в том числе три друга — Юра, Боря и Егор. Группу случайным образом разбивают на две равные подгруппы. Найдите вероятность того, что все три друга окажутся в одной группе.

Найдите корень уравнения \((x-7)^3=729\)

Найдите значение выражения \(\sqrt{27}\cos^2\dfrac{19\pi}{12}-\sqrt{27}\sin^2\dfrac{19\pi}{12}\)

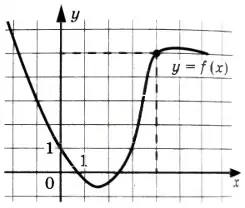
На рисунке изображён график функции \(y=f(x)\). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 4. Найдите значение производной функции в точке \(x_0=4\)

​

Расстояние (в км) от наблюдателя, находящегося на высоте \( h \) км над землёй до наблюдаемой им линии горизонта вычисляется по формуле \( l = \sqrt{2Rh} \), где \( R = 6400 \, \text{км} \) — радиус Земли. Человек, стоящий у подножия смотровой площадки видит горизонт на расстоянии 4 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 28 километров?

Каждая из двух труб с одинаковой пропускной способностью может наполнить бассейн за 11 часов. Через 3 часа после того, как одна труба наполняла бассейн, подключили вторую трубу, и бассейн наполнили две трубы вместе. Сколько часов потребовалось на наполнение бассейна?

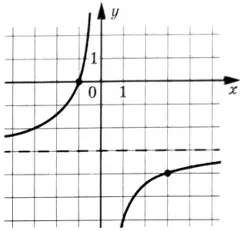
На рисунке изображён график функции \(f(x)=\dfrac{k}{x}+b\). Найдите \(f(-15)\)

​

Найдите наибольшее значение функции \( y = \dfrac13x\sqrt{x}-3x+70\) на отрезке \( [9; 81] \)

а) Решите уравнение \( 8^{1-4x}-21\cdot 4^{1,5-3x}+640=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([-1;-0{,}5]\)

Ребро \( AB \) основания \( ABCD \) правильной призмы \( ABCDA_1B_1C_1D_1 \) равно \( 2\sqrt{6} \), а высота \( AA_1 \) равна \( 2\sqrt{5} \). На рёбрах \( AB \) и \( C_1D_1 \) отметили точки \( N \) и \( K \) соответственно так, что \( N \) — середина ребра, а \( C_1K : KD_1 = 2:1 \). Через точки \( N \) и \( K \) параллельно прямой \( BD \) провели плоскость \( \alpha \).
a) Докажите, что прямая \( CA_1 \) перпендикулярна плоскости \( \alpha \).
​б) Найдите объём пирамиды с вершиной в точке \( C \) и основанием, которое образовано сечением призмы плоскостью \( \alpha \).

Решите неравенство \(\log_{0,5}\dfrac{x-3}{x+3}+2\log_4(x^2-9)\geqslant5\)

В январе 2028 года Михаил планирует открыть вклад на 3 года на целое число миллионов рублей, а в январе 2029 и 2030 годов дополнительно вносить на этот вклад ещё по 1 млн рублей. Банк предложил Михаилу два варианта условий по вкладу. В обоих вариантах условий в декабре каждого года действия вклада начисляются проценты на сумму, находящуюся на вкладе. Начисленные проценты при этом остаются на вкладе, увеличивая сумму вклада. По первому варианту процентная ставка по годам составляет 10, 15 и 20 процентов соответственно, а по второму — 20, 15 и 10 процентов. Михаил выбрал наиболее выгодное предложение. Найдите наименьший первоначальный взнос по вкладу, если при закрытии вклада через 3 года итоговая сумма должна составить не менее 11,5 млн рублей. Ответ дайте в миллионах рублей.

Точка M — середина стороны BC ромба ABCD, DB=DM.
a) Докажите, что косинус острого угла ромба равен 0,75.
б) На луче BH, где BH — высота треугольника BDM, отметили такую точку P, что в четырёхугольник ABPD можно вписать окружность. Найдите радиус этой окружности, если AB=4.

Найдите все неотрицательные значения \(a\), при каждом из которых уравнение \(|x-a|+|2x+3a|=1-ax\) имеет ровно одно решение.

Для набора 60 различных целых чисел выполнено, что сумма любых двух чисел из этого набора больше суммы любых шести чисел из этого набора.