36 вариантов ЕГЭ 2026
2 вариант ЕГЭ Ященко 2026
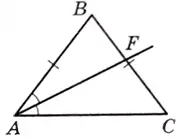
В равнобедренном треугольнике ABC с основанием AC провели биссектрису AF. Найдите угол AFB, если угол ABC равен 72°. Ответ дайте в градусах.
Даны векторы \(\vec{a}(5;-6)\) и \(\vec{b}(-5;-9)\). Найдите длину вектора \(2\vec{b}-5\vec{a}\)
Первая цилиндрическая кружка в два раза выше второй, зато вторая в два с половиной раза шире. Найдите отношение объёма второй кружки к объёму первой.
В среднем из 800 садовых насосов, поступивших в продажу, 4 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,2. Вероятность того, что кофе останется в обоих автоматах, равна 0,65. Найдите вероятность того, что к концу дня кофе закончится в обоих автоматах.
Найдите корень уравнения \(\sqrt{5x}=2\dfrac12 x\). Если уравнение имеет более одного корня, в ответе запишите больший из них.
Найдите значение выражения \(\log_a(a^3b^{14})\), если \(\log_ba=-2\)
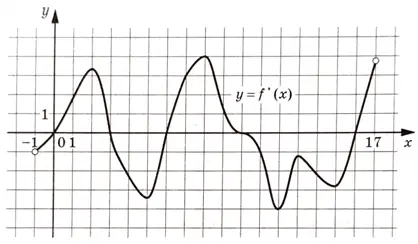
На рисунке изображён график \(y=f'(x)\) — производной функции \(f(x)\), определённой на интервале \((-1;17)\). Найдите количество точек максимума функции \(f(x)\), принадлежащих отрезку \([1;15]\)
В ходе распада радиоактивного изотопа его масса уменьшается по закону \( m=m_0\cdot2^{-\frac{t}{T}} \), где \( m_0 \) — начальная масса изотопа, \( t \) — время, прошедшее от начального момента, \( T \) — период полураспада. В начальный момент времени масса изотопа 48 мг. Период его полураспада составляет 8 минут. Найдите, через сколько минут масса изотопа будет равна 3 мг.
Баржа, скорость которой в неподвижной воде равна 15 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Скорость течения равна 1 км/ч, стоянка длится 3 часа, а в исходный пункт баржа возвращается через 18 часов после отплытия из него. Сколько километров прошла баржа за весь рейс?
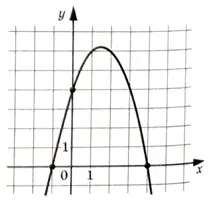
На рисунке изображен график функции \(f(x)=ax^2+bx+c\). Найдите \(f(-3)\)
Найдите точку минимума функции \(y=x^2+14\ln(x+8)+6\)
а) Решите уравнение \( \sqrt{4\sin^3x-4\cos^2x-\cos x-\sin x+3} = \sqrt{\sin\left(x-\frac{\pi}2\right)}\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{9\pi}2;6\pi\right]\)
Запишите номера всех верных ответов на пункты а) и б) по возрастанию, через запятую, без пробелов. В первое поле на пункт а), во второе - на пункт б)
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 9π/2 | 18. 14π/3 | 19. 19π/4 | 20. 29π/6 |
| 21. 5π | 22. 31π/6 | 23. 21π/4 | 24. 16π/3 |
| 25. 11π/2 | 26. 17π/3 | 27. 23π/4 | 28. 35π/6 |
| 29. 6π |
В пирамиде SABCD с высотой SA основанием является квадрат ABCD, точка K — середина ребра SB. Прямая DK пересекается с плоскостью SAC в точке N.
a) Докажите, что прямая a, проходящая через точку N параллельно прямой SC, делит диагональ основания SA в отношении 1:2.
б) Найдите угол между прямыми DK и SC, если AB=2√2, SA=3.
Решите неравенство \(\dfrac{4^x-3\cdot2^{x+1}+5}{\log_{\frac15}^2 (3^x-2)-\log_{\frac15}{(3^x-2)}^2+1}\leqslant0\)
В июне 2028 года Иван Петрович планирует взять кредит в банке на 6 лет в размере целого числа миллионов рублей. Условия его возврата таковы:
- в январе каждого года долг увеличивается на 20% от суммы долга на конец предыдущего года;
- в период с февраля по июнь в каждый из 2029, 2030, 2031 и 2032 годов необходимо выплатить только проценты по кредиту, начисленные в январе соответствующего года;
- в период с февраля по июнь в каждый из 2033 и 2034 годов платежи по кредиту равные, причём последний платёж должен погасить долг по кредиту полностью.
Найдите наименьший размер кредита, при котором общая сумма выплат по кредиту превысит 12 млн рублей.
В прямоугольную трапецию ABCD с большим основанием CD и прямыми углами A и D вписана окружность с центром в точке O радиуса R. Точка G — точка касания данной окружности и стороны AB трапеции ABCD. Биссектриса угла ADC перпендикулярна стороне BC и пересекает её в точке N.
a) Докажите, что BG=(√2-1)R.
б) Найдите радиус окружности, описанной около четырёхугольника BNOG, если R=6.
Найдите все значения \(a\), при каждом из которых система уравнений \(
\begin{cases}
\left(|x|+a^2\right)^2+(y-4a)(y+4a)=4y-4\\
0{,}5y-1=\sqrt{6a}
\end{cases}
\) имеет ровно два различных решения.
У Петра Львовича есть коллекция монет. Если все его монеты разложить в одинаковые большие классеры*, то потребуется k классеров, причём 7 ячеек в одном классере останутся пустыми. Если же их разложить в одинаковые маленькие классеры, то потребуется k+3 классеров и также 7 ячеек в одном классере останутся пустыми. Известно, что в большом классере больше 160, но меньше 170 ячеек, а в маленьком — больше 100, но меньше 120 ячеек.
*Классер — альбом (папка) для коллекционирования марок, монет.