36 вариантов ЕГЭ 2026
7 вариант ЕГЭ Ященко 2026
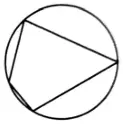
Два угла вписанного в окружность четырёхугольника равны 48° и 74°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
Даны векторы \(\vec{a}(-4;6)\) и \(\vec{b}(-2;-7)\). Найдите скалярное произведение \(\vec{a}\cdot\vec{b}\)
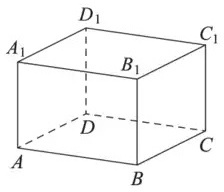
Найдите объём многогранника, вершинами которого являются точки A, B, C, A₁, B₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, у которого что AB=6, AD=9, AA₁=7.
В фирме такси в наличии 25 легковых автомобилей: 11 чёрного цвета с жёлтыми надписями на бортах, остальные — жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
Биатлонист по одному разу стреляет по пяти мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что биатлонист 4 раза попадёт в мишени и один раз промахнётся. Результат округлите до сотых.
Найдите корень уравнения \(1+\log_5(2x+17)=2\log_5(x+1)\). Если уравнение имеет больше одного корня, в ответе запишите меньший из корней.
Найдите \(\mathrm{tg\,}\alpha\), если \(\cos\alpha=\dfrac{2}{\sqrt{29}}\) и \(\alpha\in\left(\dfrac{3\pi}{2},2\pi\right)\)
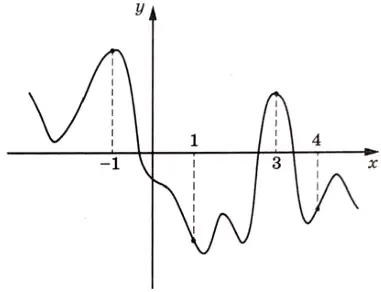
На рисунке изображён график функции \(y=f(x)\). На оси абсцисс отмечены точки -1, 1, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой \(\eta=\dfrac{T_1-T_2}{T_1}\cdot100\%\) где \(T_1\) — температура нагревателя (в кельвинах), \(T_2\) — температура холодильника (в кельвинах). При какой температуре \(T_1\) нагревателя КПД этого двигателя будет 15%, если температура холодильника \(T_2=323\,\text{К}\)? Ответ дайте в кельвинах.
Из города А в город Б выехал автобус, а через полчаса со скоростью 85 км/ч следом за ним выехал автомобиль, догнал автобус в городе К и повернул обратно. Когда автомобиль вернулся в А, автобус прибыл в Б. Найдите расстояние от А до К, если расстояние между городами А и Б равно 174 км. Ответ дайте в километрах.
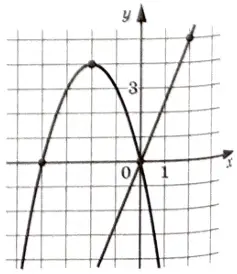
На рисунке изображены графики функций \(f(x)=kx+b\) и \(g(x)=ax^2+bx+c\), которые пересекаются в начале координат и в точке A. Найдите абсциссу точки A.
Найдите точку минимума функции \(y=(77-x)e^{77-x}\)
а) Решите уравнение \(\dfrac{\sin^4x-\sin\left(2x-\dfrac{\pi}2\right)-\cos^2x}{2\sin^2\left(\dfrac{x}4-\dfrac{\pi}4\right)+3\cos\left(\dfrac{\pi}4-\dfrac{x}4\right)-2}=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \([0;4\pi]\)
Запишите номера всех верных ответов на пункты а) и б) по возрастанию, через запятую, без пробелов. В первое поле на пункт а), во второе - на пункт б)
а)
| 1. 2πn, n∈Z | 2. π/4+πn, n∈Z | 3. π/2+πn, n∈Z | 4. 3π/4+πn, n∈Z |
| 5. π+4πn, n∈Z | 6. -π+4πn, n∈Z | |
б)
| 7. 0 | 8. π/4 | 9. π/2 | 10. 3π/4 |
| 11. π | 12. 5π/4 | 13. 3π/2 | 14. 7π/4 |
| 15. 2π | 16. 9π/4 | 17. 5π/2 | 18. 11π/4 |
| 19. 3π | 20. 13π/4 | 21. 7π/2 | 22. 15π/4 |
| 23. 4π |
В правильной треугольной призме \(ABCA_1B_1C_1\) высота \(AA_1\) в 1,25 раза больше стороны \(AB\) основания \(ABC\). Через прямую \(A_1C_1\) перпендикулярно плоскости \(ACB_1\) провели плоскость \(\alpha\).
a) Докажите, что плоскость \(\alpha\) делит ребро \(BB_1\) в отношении 12:13.
б) Найдите угол между плоскостями \(BCC_1\) и \(\alpha\).
Решите неравенство \(\sqrt{x^2-7}<1+\dfrac{4}{5-\sqrt{x^2-7}}\)
В июле 2029 года планируется взять кредит в банке на 6 лет. Условия его возврата таковы:
- в январе 2030, 2031 и 2032 годов долг возрастает на 20% по сравнению с концом предыдущего года;
- в январе 2033, 2034 и 2035 годов долг возрастает на 10% по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить часть долга;
- в июле каждого года в период с 2030 по 2034 годы долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
- в июне 2035 года необходимо выплатить 484 тысячи рублей и тем самым полностью погасить кредит.
Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 2 млн 376 тысяч рублей?
Окружность с центром в точке O радиуса R вписана в угол с вершиной в точке B, равный 60°. Точки A и C — точки касания угла и окружности, а AE и CD — диаметры окружности.
a) Докажите, что AB=DE.
б) Прямые BD и BE вторично пересекают окружность в точках N и P соответственно. Найдите площадь четырёхугольника DEPN, если R=7√3.
Найдите все значения \(a\), при каждом из которых уравнение \(\cos ax=0{,}6\) имеет на отрезке \([\pi;6\pi]\) ровно десять корней. При решении можно воспользоваться оценкой: \(0{,}92<\arccos0{,}6<0{,}93\)
На доске написаны три различных натуральных числа. Второе число равно удвоенной сумме цифр первого, а третье равно утроенной сумме цифр второго.