Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ профиль 1.20
В среднем за день во время конференции расходуется 80 пакетиков чая. Конференция длится 3 дня. В пачке чая 50 пакетиков. Какого наименьшего количества пачек чая хватит на все дни конференции?
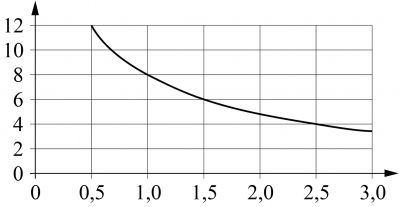
Мощность отопителя в автомобиле регулируется дополнительным сопротивлением. При этом меняется сила тока в электрической цепи электродвигателя: чем меньше сопротивление, тем больше сила тока и быстрее вращается мотор отопителя. На графике показана зависимость силы тока от величины сопротивления. На горизонтальной оси отмечено сопротивление в омах; на вертикальной оси — сила тока в амперах. Определите по графику, на сколько омов увеличилось сопротивление в цепи при уменьшении силы тока с 12 ампер до 4 ампер.
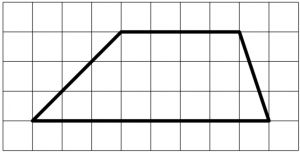
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
В сборнике 36 тренировочных вариантов ЕГЭ. В 9 из них встречается задача про окружность. На контрольной школьнику достается один случайно выбранный вариант из этого сборника. Найдите вероятность того, что в доставшемся варианте будет задача про окружность.
Найдите корень уравнения \(\sqrt{3x+49}=10\)
Треугольник ABC вписан в окружность с центром O. Угол BAC равен 24°. Найдите угол BOC. Ответ дайте в градусах.
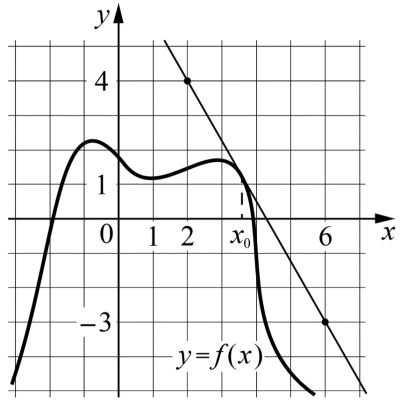
На рисунке изображены график функции \(y= f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).
Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

Найдите значение выражения \(16\log_7\sqrt[4]{7}\).
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 745 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением \(v=c\cdot\dfrac{f-f_0}{f+f_0}\), где \(c=1500\, м/с\) — скорость звука в воде, \(f_0\) — частота испускаемого сигнала (в МГц), \(f\) — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 10м/с
Смешав 55-процентный и 97-процентный растворы кислоты и добавив 10 кг чистой воды, получили 65-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 75-процентный раствор кислоты. Сколько килограммов 55-процентного раствора использовали для получения смеси?
Найдите наименьшее значение функции \(y=9x-9\ln(x+11)+7\) на отрезке [-10,5;0].
а) Решите уравнение \(4\cdot 16^{\cos x}-9\cdot 4^{\cos x}+2=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[ -2\pi;-\dfrac{\pi}2\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -2π | 18. -11π/6 | 19. -7π/4 | 20. -5π/3 |
| 21. -3π/2 | 22. -4π/3 | 23. -5π/4 | 24. -7π/6 |
| 25. -π | 26. -5π/6 | 27. -3π/4 | 28. -2π/3 |
| 29. -π/2 |
В пирамиде \(ABCD\) ребра \(DA\), \(DB\) и \(DC\) попарно перпендикулярны, а \(AB=BC=AC=14\).
а) Докажите, что эта пирамида правильная.
б) На ребрах \(DA\) и \(DC\) отмечены точки \(M\) и \(N\) соответственно, причем \(DM:MA=DN:NC=6:1\). Найдите площадь сечения \(MNB\).
Решите неравенство \(\dfrac{27^{x+\frac13}-10\cdot 9^x+10\cdot 3^x-5}{9^{x+\frac12}-10\cdot 3^x+3}\leqslant 3^x+\dfrac1{3^x-2}+\dfrac1{3^{x+1}-1}\)
В треугольнике \(ABC\) точки \(A_1\), \(B_1\) и \(C_1\) − середины сторон \(BC\), \(AC\) и \(AB\) соответственно, \(AH\) − высота, \(\angle BAC= 60°\), \(\angle BCA= 45°\).
а) Докажите, что точки \(A_1\), \(B_1\), \(C_1\) и \(H\) лежат на одной окружности.
б) Найдите \(A_1H\), если \(BC=2\sqrt3\).
Семён планирует открыть вклад на четыре года. Первоначальный вклад составляет целое число миллионов рублей. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года. Кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на 3 млн рублей. Найдите наименьший размер первоначального вклада, при котором через четыре года вклад будет больше 20 млн рублей. Ответ дайте в миллионах рублей.
Найдите все значения параметра \(a\), при которых уравнение \(\sqrt{1-2x}=a-3|x|\) имеет более двух решений.
\(a\), \(b\), \(c\) и \(d\) – попарно различные двузначные положительные числа.
а) Может ли выполняться равенство \(\dfrac{a+c}{b+d}=\dfrac7{19}\)?
б) Может ли дробь \(\dfrac{a+c}{b+d}\) быть в 11 раз меньше, чем сумма \(\dfrac{a}{b}+\dfrac{c}{d}\)?
в) Какое наименьшее значение может принимать дробь \(\dfrac{a+c}{b+d}\), если \(a>3b\) и \(c>6d\)?
Введите ответ в форме строки "да;да;23:34", где ответы на пункты разделены ";", первые два ответа с маленькой буквы, а ответ на пункт в) в виде несократимого отношения, записанного через ":".