Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ 24.18 (1-12; 18)
\(\boxed{1}\) Для приготовления маринада для огурцов на 1 литр воды требуется 15 г лимонной кислоты. Лимонная кислота продается в пакетиках по 25 г. Какое наименьшее число пакетиков нужно купить хозяйке для приготовления 9 литров маринада?
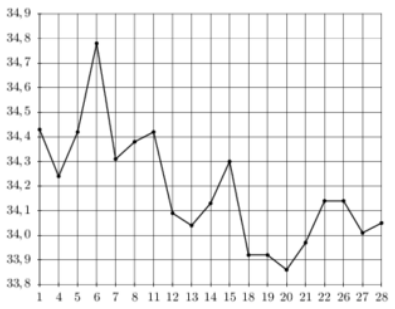
\(\boxed{2}\) На рисунке жирными точками показан курс доллара, установленный центробанком РФ во все рабочие дни в феврале некоторого года. В выходные цена не менялась. По горизонтали указываются числа месяца, по вертикали – цена доллара в рублях. Для наглядности жирыне точки на рисунке соединены линией. Определите по рисунку, сколько было рабочих дней за указанный период, когда цена доллара была меньше \(34{,}3\) рублей.
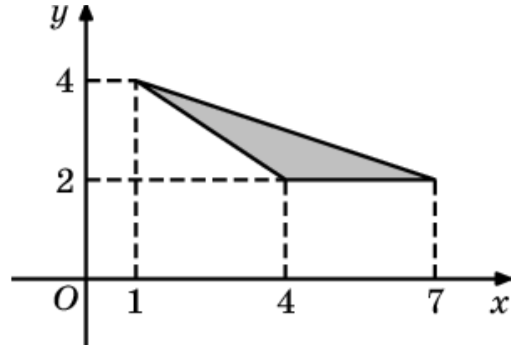
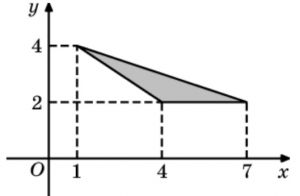
\(\boxed{3}\) Найдите площадь треугольника, изображенного на рисунке.
\(\boxed{4}\) В сборнике билетов по химии всего 40 билетов, в 18 из них встречается вопрос по теме "Кислоты". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме "Кислоты".
\(\boxed{5}\) Решите уравнение \(\dfrac6{13}x^2=19\dfrac12\). Если корней несколько, в ответ запишите меньший из них.
\(\boxed{6}\) Хорда \(AB\) делит окружность на две дуги, градусные меры которых относятся как \(2 : 7\). Под каким углом видна эта хорда из точки \(C\), принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
\(\boxed{7}\) Материальная точка движется прямолинейно по закону \( x(t)=t^2-2t-11\), где \(x\) – расстояние от точки отсчета (в метрах), \(t\) – время в секундах, прошедшее с начала движения. Найдите её скорость (в м/с) в момент времени \(t=5c\).
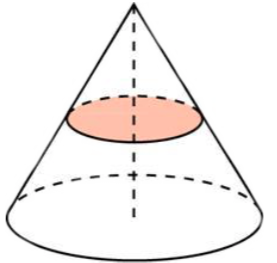
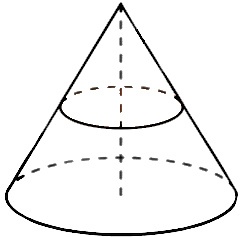
\(\boxed{8}\) Площадь полной поверхности конуса равна 24. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
\(\boxed{9}\) Найдите значение выражения \(\dfrac{8\cos\alpha-2\sin\alpha+12}{\sin\alpha-4\cos\alpha+6}\), если \(\mathrm{tg\,}\alpha=4\).
\(\boxed{10}\) В розетку электросети подключены приборы, общее сопротивление которых составляет \(R_1=72\, Ом\). Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление \(R_2\) этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями \(R_1\, Ом\) и \(R_2\, Ом\) их общее сопротивление вычисляется по формуле \(R_{общ}=\dfrac{R_1 R_2}{R_1+R_2}\, (Ом) \), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 18 Ом. Ответ выразите в Омах.
\(\boxed{11}\) В 2015 году в городском квартале проживало 40000 человек. В 2016 году, в результате строительства новых домов, число жителей выросло на 7%, а в 2017 году – на 8% по сравнению с 2016 годом. Сколько человек стало проживать в квартале в 2017 году?
\(\boxed{12}\) Найдите наименьшее значение функции \( y=(x-8)^2(x-1)+20\) на отрезке \([7;13]\).
\(\boxed{18}\) Найдите все значения параметра \(a\), при которых уравнение \(6^{100x^2-60x+10}+16a^2+40a+20+\sin(5\pi x)=0\) имеет хотя бы одно решение. И укажите корни уравнения для каждого найденного значения \(a\).
Для приготовления маринада для огурцов на 1 литр воды требуется 15 г лимонной кислоты. Лимонная кислота продается в пакетиках по 25 г. Какое наименьшее число пакетиков нужно купить хозяйке для приготовления 9 литров маринада?
На рисунке жирными точками показан курс доллара, установленный центробанком РФ во все рабочие дни в феврале некоторого года. В выходные цена не менялась. По горизонтали указываются числа месяца, по вертикали – цена доллара в рублях. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько было рабочих дней за указанный период, когда цена доллара была меньше \(34{,}3\) рублей.
![]()
Найдите площадь треугольника, изображенного на рисунке.
В сборнике билетов по химии всего 40 билетов, в 18 из них встречается вопрос по теме "Кислоты". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме "Кислоты".
Решите уравнение \(\dfrac6{13}x^2=19\dfrac12\). Если корней несколько, в ответ запишите меньший из них.
Хорда AB делит окружность на две дуги, градусные меры которых относятся как 2:7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
Материальная точка движется прямолинейно по закону \( x(t)=t^2-2t-11\), где \(x\) – расстояние от точки отсчета (в метрах), \(t\) – время в секундах, прошедшее с начала движения. Найдите её скорость (в м/с) в момент времени \(t=5c\).
Площадь полной поверхности конуса равна 24. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.
Найдите значение выражения \(\dfrac{8\cos\alpha-2\sin\alpha+12}{\sin\alpha-4\cos\alpha+6}\), если \(\mathrm{tg\,}\alpha=4\)
В розетку электросети подключены приборы, общее сопротивление которых составляет \(R_1=72\, Ом\). Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление \(R_2\) этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями \(R_1\, Ом\) и \(R_2\, Ом\) их общее сопротивление вычисляется по формуле \(R_{общ}=\dfrac{R_1 R_2}{R_1+R_2}\, (Ом) \), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 18 Ом. Ответ выразите в Омах.
В 2015 году в городском квартале проживало 40000 человек. В 2016 году, в результате строительства новых домов, число жителей выросло на 7%, а в 2017 году – на 8% по сравнению с 2016 годом. Сколько человек стало проживать в квартале в 2017 году?
Найдите наименьшее значение функции \( y=(x-8)^2(x-1)+20\) на отрезке \([7;13]\).
Найдите все значения параметра \(a\), при которых уравнение \(6^{100x^2-60x+10}+16a^2+40a+20+\sin(5\pi x)=0\) имеет хотя бы одно решение. И укажите корни уравнения для каждого найденного значения \(a\).