Вариант ЕГЭ 29.18 (1-12)

Цена на электрический чайник была повышена на 23% и составила 2337 рублей. Сколько рублей стоил чайник до повышения цены?

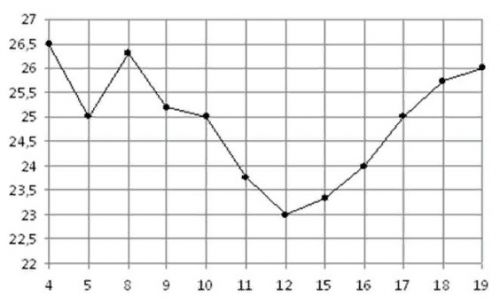
На рисунке жирными точками показана цена нефти на момент закрытия биржевых торгов во все рабочие дни с 4 по 19 марта 2003 года. По горизонтали указываются числа месяца, по вертикали – цена барреля нефти в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена нефти на момент закрытия торгов была наибольшей за данный период.

​

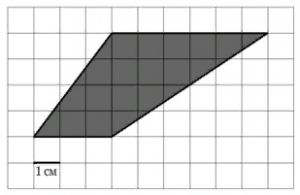
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

​

В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. 4 мая погода в Волшебной стране хорошая. Найдите вероятность того, что 7 мая в Волшебной стране будет отличная погода.

Найдите корень уравнения \(\log_6(5 - x)=2\).

Два угла вписанного в окружность четырёхугольника равны 29° и 57°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

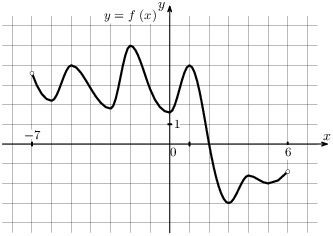
На рисунке изображен график функции \(y = f(x)\), определённой на интервале (-7;6). Найдите сумму точек экстремума функции \(f(x)\).

Если каждое ребро куба увеличить на 5, то его площадь поверхности увеличится на 270. Найдите ребро куба.

Найдите значение выражения \((397^2 – 78^2) : 475\).

В телевизоре ёмкость высоковольтного конденсатора \(C = 6⋅10^{-6}\, Ф\). Параллельно с конденсатором подключён резистор с сопротивлением \(R = 6⋅10^{6}\, Ом\). Во время работы телевизора напряжение на конденсаторе \(U_0=26\, кВ\). После включения телевизора напряжение на конденсаторе убывает до значения \(U\,(кВ)\)за время, определяемое выражением \(t = aRC\log_{2}{\frac{U_0}{U}}\) (с), где \(a = 1{,}2 \) – постоянная. Определите напряжение на конденсаторе, если после включения телевизора прошло 43,2 с. Ответ дайте в киловольтах

Из одной точки круговой трассы, длина которой равна 25 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 112 км/ч, и через 25 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Найдите наибольшее значение функции \(y = -3x^{5} - 6x^{3} + 14\) на отрезке [-1;8].