Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ 20.18 (1-12)
Разбор варианта
\( \boxed{1}\) Батон хлеба стоит 66 рублей. Владельцам карт магазина предоставляеся скидка 5%. Сколько рублей стоит батон хлеба для владельца такой карты?
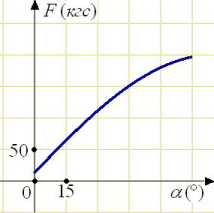
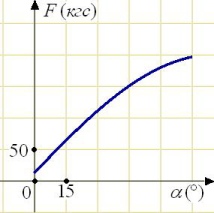
\( \boxed{2}\) В аэропорту чемоданы пассажиров поднимают в зал выдачи багажа по транспортерной ленте. При проектировании транспортера необходимо учитывать допустимую силу натяжения ленты транспортера. На рисунке изображена зависимость натяжения ленты от угла наклона транспортера к горизонту при расчетной нагрузке. На оси абсцисс откладывается угол подъема в градусах, на оси ординат – сила натяжения транспортерной ленты (в килограммах силы). При каком угле наклона сила натяжения достигает 150 кгс? Ответ дайте в градусах.
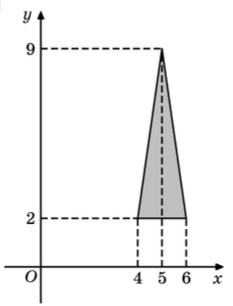
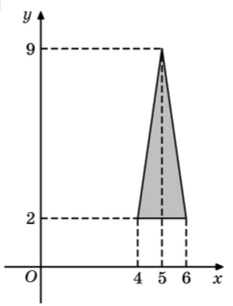
\( \boxed{3}\) Найдите площадь треугольника, изображенного на рисунке.
\( \boxed{4}\) В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,25. Вероятность того, что чай закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.
\( \boxed{5}\) Решите уравнение \(\sqrt{4x-3}=x\). Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
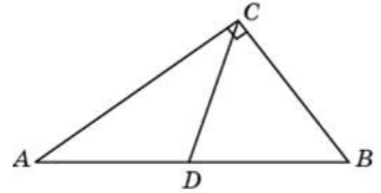
\( \boxed{6}\) В треугольнике \(ABC\) угол \(ACB\) прямой, угол \(ABC\) равен 18°, \(CD\) – медиана. Найдите угол \(ACD\). Ответ дайте в градусах.
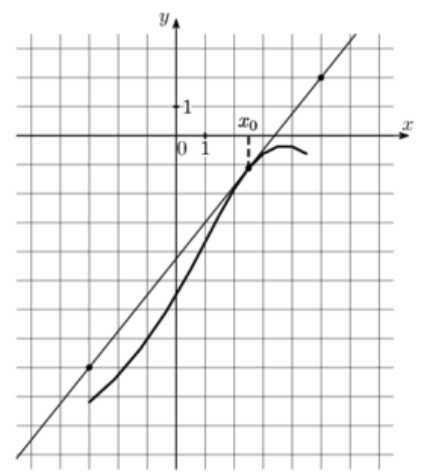
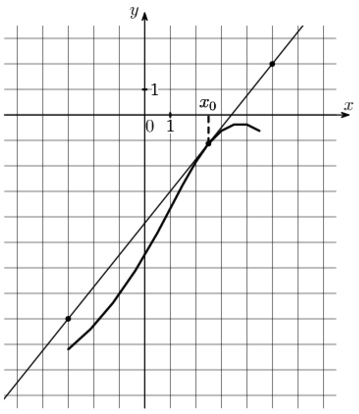
\( \boxed{7}\) На рисунке изображены график функции \(y=f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).
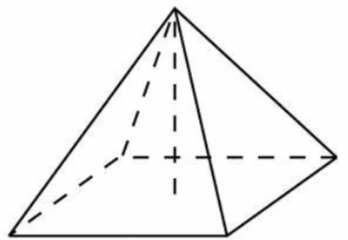
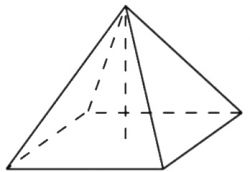
\( \boxed{8}\) Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 и высота равна 4.
\( \boxed{9}\) Найдите \( \cos \alpha\), если \( \sin \alpha=-\dfrac{24}{25}\) и \(\alpha\in \Big( \dfrac{3\pi}{2};2\pi \Big) \).
\( \boxed{10}\) В установке для демонстрации адиабатического сжатия газа поршень сжимает газ в сосуде. При этом объем и давление связаны соотношением \(pV^{1{,}4}=cosnt\), где \(p\) – давление газа (в атмосферах), \(V\) – объем газа (в литрах). Изначально, объем газа равен 224 л, а его давление равно одной атмосфере. До какого объема надо сжать газ, чтобы давление стало равным 128 атмосфер? Ответ дайте в литрах.
\( \boxed{11}\) Имеется два сосуда. Первый содержит 100 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 67% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 77% кислоты. Сколько килограммов кислоты содержится во втором сосуде?
\( \boxed{12}\) Найдите точку минимума функции \( y=-\dfrac{x^2+324}{x} \).
Ответы
1) 62,7
2) 45
3) 7
4) 0,7
5) 1
6) 72
7) 1,25
8) 60
9) 0,28
10) 7
11) 18,4
12) -18
Батон хлеба стоит 66 рублей. Владельцам карт магазина предоставляется скидка 5%. Сколько рублей стоит батон хлеба для владельца такой карты?
В аэропорту чемоданы пассажиров поднимают в зал выдачи багажа по транспортерной ленте. При проектировании транспортера необходимо учитывать допустимую силу натяжения ленты транспортера. На рисунке изображена зависимость натяжения ленты от угла наклона транспортера к горизонту при расчетной нагрузке. На оси абсцисс откладывается угол подъема в градусах, на оси ординат – сила натяжения транспортерной ленты (в килограммах силы). При каком угле наклона сила натяжения достигает 150 кгс? Ответ дайте в градусах.
Найдите площадь треугольника, изображенного на рисунке.
В торговом центре два одинаковых автомата продают чай. Вероятность того, что к концу дня в автомате закончится чай, равна 0,25. Вероятность того, что чай закончится в обоих автоматах, равна 0,2. Найдите вероятность того, что к концу дня чай останется в обоих автоматах.
Решите уравнение \(\sqrt{4x-3}=x\). Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
В треугольнике \(ABC\) угол \(ACB\) прямой, угол \(ABC\) равен 18°, \(CD\) – медиана. Найдите угол \(ACD\). Ответ дайте в градусах.
На рисунке изображены график функции \(y=f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).
Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 и высота равна 4.
Найдите \( \cos \alpha\), если \( \sin \alpha=-\dfrac{24}{25}\) и \(\alpha\in \Big( \dfrac{3\pi}{2};2\pi \Big) \).
В установке для демонстрации адиабатического сжатия газа поршень сжимает газ в сосуде. При этом объем и давление связаны соотношением \(pV^{1{,}4}=const\), где \(p\) – давление газа (в атмосферах), \(V\) – объем газа (в литрах). Изначально, объем газа равен 224 л, а его давление равно одной атмосфере. До какого объема надо сжать газ, чтобы давление стало равным 128 атмосфер? Ответ дайте в литрах.
Имеется два сосуда. Первый содержит 100 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 67% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 77% кислоты. Сколько килограммов кислоты содержится во втором сосуде?
Найдите точку минимума функции \( y=-\dfrac{x^2+324}{x} \).