Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ профиль 5.19
\(\boxed{1}\) Диагональ экрана телевизора равна 65 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см.
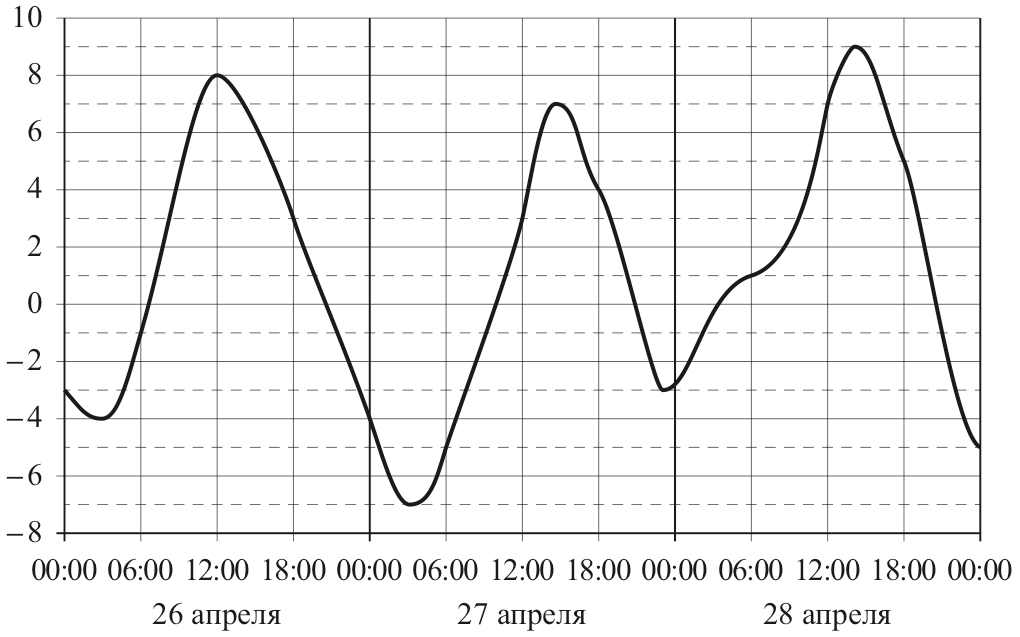
\(\boxed{2}\) На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 28 октября. Ответ дайте в градусах Цельсия.
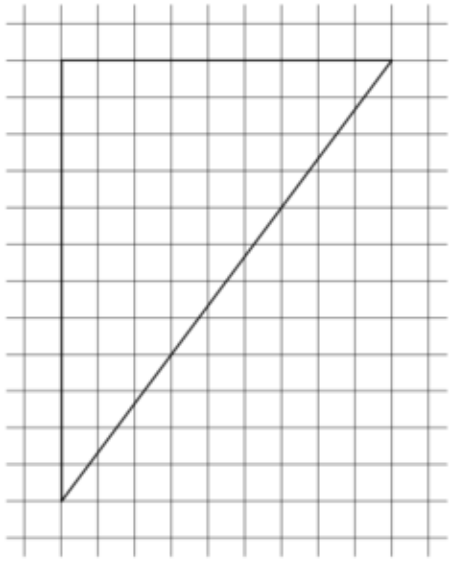
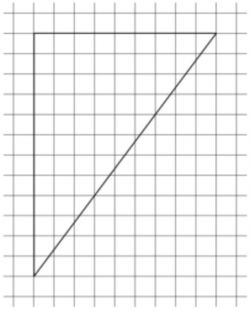
\(\boxed{3}\) Найдите гипотенузу прямоугольного треугольника, изображенного на клетчатой бумаге, если размер клетки 1×1.
\(\boxed{4}\) Научная конференция проводится в 3 дня. Всего запланировано 40 докладов. В первый день 24 доклада, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на второй день конференции?
\(\boxed{5}\) Решите уравнение \( (x-4)^3=343\).
\(\boxed{6}\) Стороны параллелограмма равны 15 и 10. Высота, опущенная на одну сторону, равна 12. Найдите высоту, опущенную на другую сторону параллелограмма.
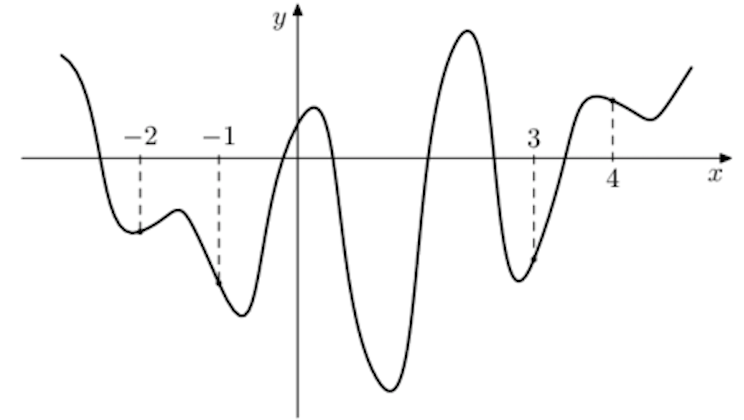
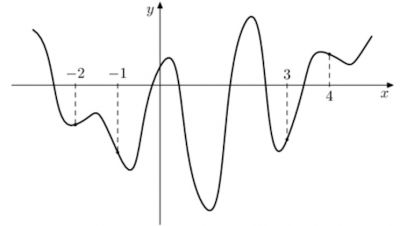
\(\boxed{7}\) На рисунке изображен график функции \(y = f (x)\) и отмечены точки –2, –1, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
\(\boxed{8}\) Даны два цилинтра. Объем первого цилиндра равен 18. У второго цилиндра высота в 2 раза больше а радиус основания в 1,5 раза меньше чем у первого. Найдите объем второго цилиндра.
\(\boxed{9}\) Найдите значение выражения \( \dfrac{12\sin146°}{\sin 73°\cdot \sin 17°}\).
\(\boxed{10}\) Водолазный колокол, содержащий \(\nu=5\) моля воздуха при давлении \(p_1=1{,}2\) атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления \(p_2\). Работа, совершаемая водой при сжатии воздуха, определяется выражением \(A=\alpha \nu T \log_2{\dfrac{p_2}{p_1}}\), где \(\alpha=19{,}1\, \dfrac{Дж}{моль\cdot К}\) – постоянная, \(T=300\, К\) – температура воздуха. Найдите, какое давление \(p_2\) (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 28650 Дж.
\(\boxed{11}\) Теплоход проходит по течению реки до пункта назначения 775 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 28 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 61 час после отплытия из него. Ответ дайте в км/ч.
\(\boxed{12}\) Найдите наименьшее значение функции \(y=(x^2-9x+9)e^{x}\) на отрезке \([-5;3]\).
\(\boxed{13}\) а) Решите уравнение \(\dfrac{\sin x}{2\cos^2{\dfrac{x}2}}=4\sin^2{\dfrac{x}2}\).
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\Big[ -\dfrac{7\pi}{2};-2\pi\Big]\).
\(\boxed{14}\) Дана правильная четырехугольная призма \(ABCDA_1B_1C_1D_1\). На ребре \(AA_1\) отмечена точка \(K\) так, что \(AK:KA_1=1:3\). Плоскость \(\alpha\) проходит через точки \(B\), \(K\) параллельно прямой \(AC\). Эта плоскость пересекает ребро \(DD_1\) в точке \(M\).
а) Докажите, что M – середина ребра \(DD_1\).
б) Найдите площадь сечения призмы плоскостью \(\alpha\), если \(AB=5\), \(AA_1=4\).
\(\boxed{15}\) Решите неравенство \(\dfrac{6^x-4\cdot 3^x}{x\cdot 2^x-5\cdot 2^x-4x+20}\leqslant \dfrac{1}{x-5}\).
\(\boxed{16}\) Высоты тупоугольного треугольника \(ABC\) с тупым углом \(ABC\) пересекаются в точке \(H\). Угол \(AHC\) равен 60°.
а) Докажите, что угол \(ABC\) равен 120°.
б) Найдите \(BH\), если \(AB=6\), \(BC=10\).
\(\boxed{17}\) В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
— в январе каждого года долг увеличивается на 25% по сравнению с предыдущим годом;
— с февраля по июнь нужно выплатить часть долга одним платежом. Определите, какую сумму взяли в кредит, если известно, что кредит был выплачен тремя равными платежами (то есть за 3 года) и общая сумма выплат составила 187500 рублей.
\(\boxed{18}\) Найдите все значения параметра \(a\), при каждом из которых система
\(\begin{cases} ((x-6)^2+y^2-a^2)\ln(16-x^2-y^2)=0 \\ ((x-6)^2+y^2-a^2)(y-x+a-6)=0 \end{cases}\)
имеет ровно два различных решения.
\(\boxed{19}\) На доске написано \(n\) чисел \(a_i\) (\(i = 1,2, ..., n\)). Каждое из чисел не меньше 50 и не больше 150. Каждое из этих чисел уменьшают на \(r_i\%\) (для каждого числа какой-то процент). При этом, для каждого \(i\) (\(1\leqslant 1 \leqslant n\)) либо \(r_i = 4\), либо число \(a\) уменьшается на 4, то есть становится равным \(a_i - 4\).
а) Может ли среднее арифметическое чисел \(r_1, r_2, ..., r_n\) быть равным 10?
б) Могло ли оказаться, что среднее арифметическое чисел \(r_1, r_2, ...,r_i\) больше 4, а сумма чисел \(а_1, а_2, ..., а_n\) уменьшилась менее чем на \(4n\)?
в) Пусть всего чисел 20, а после выполнения описанной операции их сумма уменьшилась на 50. Найдите наибольшее возможное значение среднего арифметического чисел \(r_1, r_2, ..., r_n\).
Ответы
1) 165,1
2) -5
3) 15
4) 0,2
5) 11
6) 8
7) -1
8) 16
9) 24
10) 2,4
11) 3
12) 9
13) а) \(2\pi n; \dfrac{\pi}{6}+2\pi k; \dfrac{5\pi}{6}+2\pi m,\; n,k,m\in\mathbb{Z}\)
б) \(-\dfrac{19\pi}{6}; -2\pi\)
14) \(15\sqrt{3}\)
15) \( [0;2)\cup (2;5) \)
16) \(\dfrac{14}{\sqrt{3}}\)
17) 122000
18) \( (6-\sqrt{30};2]\cup [10;6+\sqrt{30}) \)
19) а) Нет
б) Да. Например, если \(a_1=a_2=50;\, r_1=8, r_2=4\)
в) 5
Диагональ экрана телевизора равна 65 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см.
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 28 апреля. Ответ дайте в градусах Цельсия.
Найдите гипотенузу прямоугольного треугольника, изображенного на клетчатой бумаге, если размер клетки 1×1.
Научная конференция проводится в 3 дня. Всего запланировано 40 докладов. В первый день 24 доклада, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на второй день конференции?
Решите уравнение \( (x-4)^3=343\).
Стороны параллелограмма равны 15 и 10. Высота, опущенная на одну сторону, равна 12. Найдите высоту, опущенную на другую сторону параллелограмма.
На рисунке изображен график функции \(y = f (x)\) и отмечены точки –2, –1, 3, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Даны два цилиндра. Объем первого цилиндра равен 18. У второго цилиндра высота в 2 раза больше, а радиус основания в 1,5 раза меньше, чем у первого. Найдите объем второго цилиндра.
Найдите значение выражения \( \dfrac{12\sin146°}{\sin 73°\cdot \sin 17°}\).
Водолазный колокол, содержащий \(\nu=5\) моль воздуха при давлении \(p_1=1{,}2\) атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления \(p_2\). Работа, совершаемая водой при сжатии воздуха, определяется выражением \(A=\alpha \nu T \log_2{\dfrac{p_2}{p_1}}\), где \(\alpha=19{,}1\, \dfrac{Дж}{моль\cdot К}\) – постоянная, \(T=300\, К\) – температура воздуха. Найдите, какое давление \(p_2\) (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в \(28650 \,Дж\).
Теплоход проходит по течению реки до пункта назначения 775 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 28 км/ч, стоянка длится 5 часов, а в пункт отправления теплоход возвращается через 61 час после отплытия из него. Ответ дайте в км/ч.
Найдите наибольшее значение функции \(y=(x^2-9x+9)e^{x}\) на отрезке \([-5;3]\).
а) Решите уравнение \(\dfrac{\sin x}{2\cos^2{\dfrac{x}2}}=4\sin^2{\dfrac{x}2}\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[ -\dfrac{7\pi}{2};-2\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17.-7π/2 | 18. -10π/3 | 19. -13π/4 | 20. -19π/6 |
| 21. -3π | 22. -17π/6 | 23. -11π/4 | 24. -8π/3 |
| 25.-5π/2 | 26. -7π/3 | 27. -9π/4 | 28. -13π/6 |
| 29. -2π |
Дана правильная четырехугольная призма \(ABCDA_1B_1C_1D_1\). На ребре \(AA_1\) отмечена точка \(K\) так, что \(AK:KA_1=1:3\). Плоскость \(\alpha\) проходит через точки \(B\), \(K\) параллельно прямой \(AC\). Эта плоскость пересекает ребро \(DD_1\) в точке \(M\).
а) Докажите, что M – середина ребра \(DD_1\).
б) Найдите площадь сечения призмы плоскостью \(\alpha\), если \(AB=5\), \(AA_1=4\).
Решите неравенство \(\dfrac{6^x-4\cdot 3^x}{x\cdot 2^x-5\cdot 2^x-4x+20}\leqslant \dfrac{1}{x-5}\)
Высоты тупоугольного треугольника ABC с тупым углом ABC пересекаются в точке H. Угол AHC равен 60°.
а) Докажите, что угол ABC равен 120°.
б) Найдите BH, если AB=6, BC=10.
В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы:
— в январе каждого года долг увеличивается на 25% по сравнению с предыдущим годом;
— с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, какую сумму взяли в кредит, если известно, что кредит был выплачен тремя равными платежами (то есть за 3 года) и общая сумма выплат составила 187500 рублей.
Найдите все значения параметра \(a\), при каждом из которых система \(\begin{cases} ((x-6)^2+y^2-a^2)\ln(16-x^2-y^2)=0 \\ ((x-6)^2+y^2-a^2)(y-x+a-6)=0 \end{cases}\) имеет ровно два различных решения.
На доске написано \(n\) чисел \(a_i\) (\(i = 1,2, ..., n\)). Каждое из чисел не меньше 50 и не больше 150. Каждое из этих чисел уменьшают на \(r_i\%\) (для каждого числа какой-то процент). При этом, для каждого \(i\) (\(1\leqslant 1 \leqslant n\)) либо \(r_i = 4\), либо число \(a\) уменьшается на 4, то есть становится равным \(a_i - 4\).
а) Может ли среднее арифметическое чисел \(r_1, r_2, ..., r_n\) быть равным 10?
б) Могло ли оказаться, что среднее арифметическое чисел \(r_1, r_2, ...,r_i\) больше 4, а сумма чисел \(а_1, а_2, ..., а_n\) уменьшилась менее чем на \(4n\)?
в) Пусть всего чисел 20, а после выполнения описанной операции их сумма уменьшилась на 50. Найдите наибольшее возможное значение среднего арифметического чисел \(r_1, r_2, ..., r_n\).
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.