Вариант ЕГЭ 10.18 (1-12;18)

Диагональ экрана телевизора равна 42 дюймам. Чему равна диагональ экрана в сантиметрах, если один дюйм равен 2,54 см? Результат округлите до целого числа.

На диаграмме показано количество посетителей сайта во все дни с 10 по 29 марта 2001 года. По горизонтали указываются дни месяца, по вертикали - количество посетителей сайта за данный день. Каким было наименьшее суточное количество посетителей сайта указанный период?

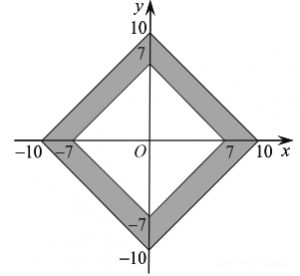
Найдите площадь закрашенной фигуры на координатной плоскости.

Вероятность того, что новый чайник в течение года поступит в гарантийный ремонт, равна 0,076. В некотором магазине из 1000 проданных чайников в течение года в гарантийную мастерскую поступило 96 штук. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом магазине?

Найдите корень уравнения: \(7^{3-2x}=0,49\cdot10^{3-2x}\).

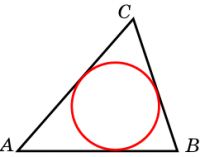
Периметр треугольника равен 62, а радиус вписанной окружности равен 5. Найдите площадь этого треугольника.

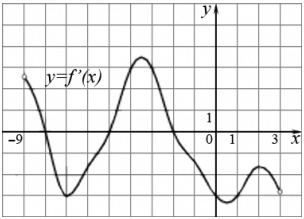
На рисунке изображен график \(y=f'(x)\) – производной функции \(y=f(x)\), определенной на интервале (-9;3). Найдите количество точек, в которых касательная к графику функции \(y=f(x)\) параллельна прямой \(y=2x-23\) или совпадает с ней.

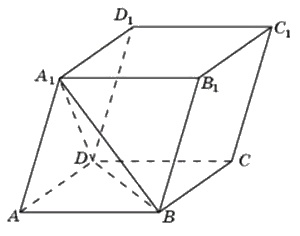
Объём параллелепипеда ABCDA₁B₁C₁D₁ равен 24. Найдите объём треугольной пирамиды ABDA₁.

Найдите значение выражения \(\dfrac{15}{\sin\left({-\dfrac{25\pi}{4}}\right)\cdot\cos\left({\dfrac{25\pi}{4}}\right)}\)

В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах меняется по закону \(H(t) = at^{2}+bt+H_{0}\), где \(H_{0}= 9 м\) - начальный уровень воды, \(a = \dfrac{1}{196} м/мин^{2}\), \(b = -\dfrac{3}{7} м/мин \) - постоянные, \(t\) - время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.

Двое рабочих, работая вместе, могут выполнить работу за 2 дня. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за 1 день выполняет такую же часть работы, какую второй - за 2 дня?

Найдите точку минимума функции \(y= x^{3}-108x+42\).

Найдите все значения параметра \(a\), при которых все корни уравнения \(ax^{2}+2(2-a)x+1=0\) удовлетворяют условия \(|x| < 1\).