Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ профиль 3.20
Держатели дисконтной карты книжного магазина получают при покупке скидку 5%. Книга стоит 500 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
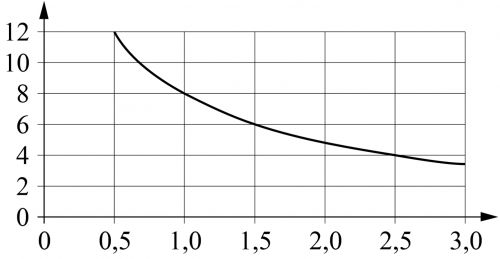
Мощность отопителя в автомобиле регулируется дополнительным сопротивлением, которое можно менять, поворачивая рукоятку в салоне машины. При этом меняется сила тока в электрической цепи электродвигателя — чем меньше сопротивление, тем больше сила тока и тем быстрее вращается мотор отопителя. На рисунке показана зависимость силы тока от величины сопротивления. На оси абсцисс откладывается сопротивление (в омах), на оси ординат — сила тока в амперах. На сколько ампер уменьшится сила тока, если увеличить сопротивление с 0,5 Ом до 2,5 Ом?
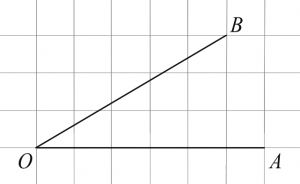
На клетчатой бумаге с размером клетки 1×1 изображён угол. Найдите тангенс этого угла.
В группе туристов 20 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 5 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист Ф. полетит вторым рейсом вертолёта.
Найдите корень уравнения \((x+3)^3=-8\).
Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
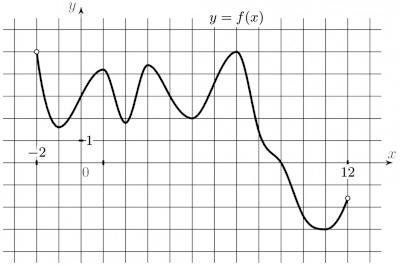
На рисунке изображён график функции \(y=f(x)\), определённой на интервале (-2;12). Найдите количество точек, в которых производная функции \(f(x)\) равна 0.
В правильной четырёхугольной призме \(ABCDA_1B_1C_1D_1\) ребро \(AA_1\) равно 15, а диагональ \(BD_1\) равна 25. Найдите площадь сечения призмы плоскостью, проходящей через точки \(A\), \(A_1\) и \(C\).
Найдите значение выражения \(\dfrac{3^{6{,}2}}{9^{1{,}6}}\).
После дождя уровень воды в колодце может повыситься. Мальчик измеряет время \(t\) падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле \(h=5t^2\), где \(h\) — расстояние в метрах, \(t\) — время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
Первый садовый насос перекачивает 9 литров воды за 4 минуты, второй насос перекачивает тот же объём воды за 6 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 30 литров воды?
Найдите наименьшее значение функции \(y=15+12x+x^3\) на отрезке \([-2;2]\).
а) Решите уравнение \((1-3\mathrm{tg\,}^2x)\sqrt{7\sin x}=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезок \(\left[-\dfrac{7\pi}2;-2\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17.-7π/2 | 18. -10π/3 | 19. -13π/4 | 20. -19π/6 |
| 21. -3π | 22. -17π/6 | 23. -11π/4 | 24. -8π/3 |
| 25.-5π/2 | 26. -7π/3 | 27. -9π/4 | 28. -13π/6 |
| 29. -2π |
В основании прямой треугольной призмы ABCA₁B₁C₁ лежит равнобедренный треугольник ABC с равными сторонами AB и BC. Точки K и M — середины рёбер A₁B₁ и AC соответственно.
а) Докажите, что KM=KB.
б) Найдите угол между прямой KM и плоскостью ABB₁, если AB=8, AC=6 и AA₁=3.
Решите неравенство \(\dfrac{2^{2x+2}-9\cdot 2^{x+2}+32}{2^{x+3}-2^{2x}}\leqslant \dfrac{3}{2^{x}}\).
В треугольнике ABC проведены биссектрисы BM и CN. Оказалось, что точки B, C, M и N лежат на одной окружности.
а) Докажите, что треугольник ABC равнобедренный.
б) Пусть P — точка пересечения биссектрис треугольника ABC. Найдите площадь четырёхугольника AMPN, если MN:BC=2:5, а BN=14.
По вкладу «А» банк в конце каждого года планирует увеличивать на 10% сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать эту сумму на 8% в первый год и на одинаковое целое число n процентов и за второй, и за третий годы. Найдите наименьшее значение n, при котором за три года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Найдите все значения параметра \(a\), при которых система
\(\begin{cases} x^2+y^2+5=2(2x+y)\\a^2+ax+2ay=5\end{cases}\)
имеет решение.
Запишите ответы по возрастанию через точку с запятой без пробелов.
Будем называть четырёхзначное число интересным, если среди четырёх цифр в его десятичной записи нет нулей, а одна из этих цифр равна сумме трёх других из них. Например, интересным является число 3111.
а) Найдутся ли два интересных четырёхзначных числа, разность между которыми равна 17?
б) Найдутся ли два интересных четырёхзначных числа, разность между которыми равна 109?
в) Найдите наименьшее простое число, для которого не существует кратного ему интересного четырёхзначного числа.
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.