Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ 22.18 (1-12; 13; 15)
\(\boxed{1}\) Набор скрепок стоит 60 рублей. Какое наибольшее количество таких наборов можно будет купить на 850 рублей после понижения цены на 25%?
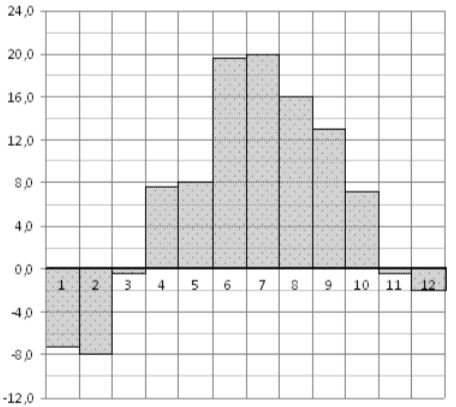
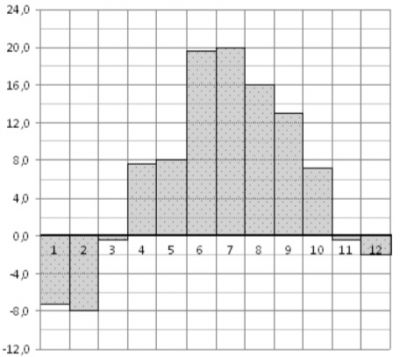
\(\boxed{2}\) На диаграмме показана среднемесячная температура воздуха в городе N за каждый месяц некоторого года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме, сколько за этот год было месяцев с положительной среднемесячной температурой.
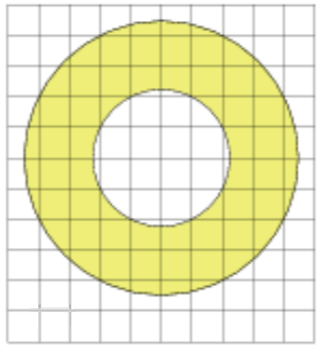
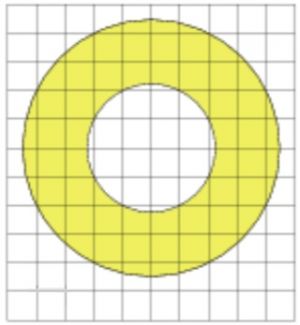
\(\boxed{3}\) Найдите (в см\(^2\)) площадь \(S\) кольца, изображённого на клетчатой бумаге с размером клетки 2 см × 2 см (см. рис.). В ответе запишите \(\dfrac{S}{\pi}\).
\(\boxed{4}\) Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью \(0{,}8\). Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью \( 0{,}02\). Известно, что 76% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
\(\boxed{5}\) Найдите корень уравнения \(\log_{81}3^{2x-3}=3\).
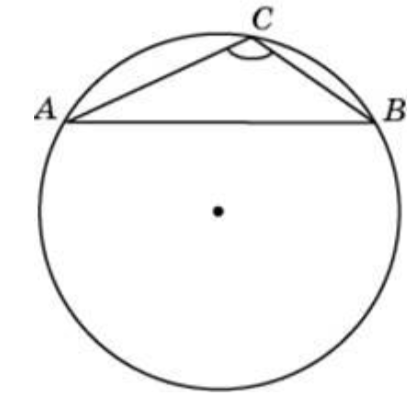
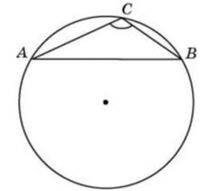
\(\boxed{6}\) Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса \(23\sqrt3\).
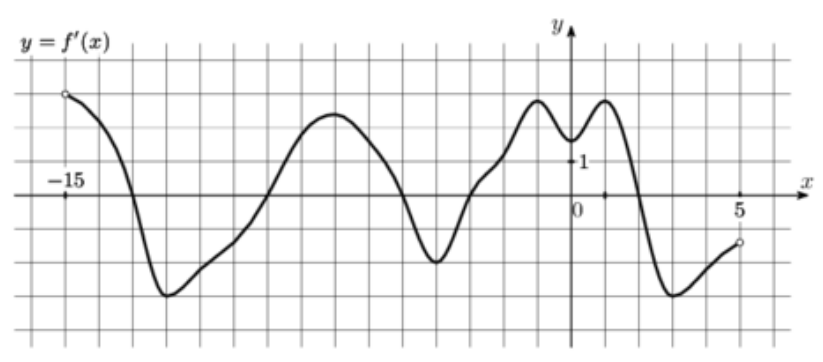
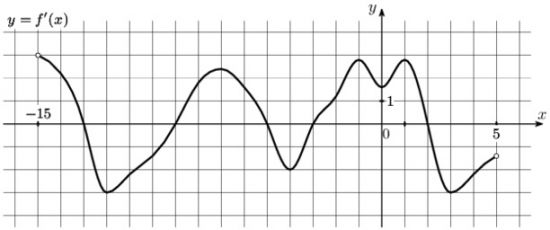
\(\boxed{7}\) На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\), определенной на интервале \((-15;5)\). Найдите количество точек максимума функции \(f(x)\) принадлежащих отрезку \([-12;3]\).
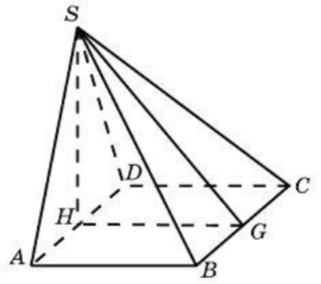
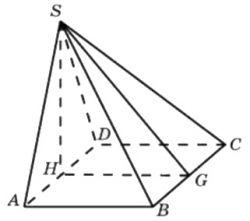
\(\boxed{8}\) Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 9. Найдите объем пирамиды.
\(\boxed{9}\) Найдите значение выражения \(\left(\dfrac{7^{\frac12}\cdot 7^{\frac13}}{\sqrt[6]{7}}\right)^3 \).
\(\boxed{10}\) Сила тока в цепи \(I\) (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: \(I=\dfrac{U}{R}\), где \(U\) – напряжение в вольтах, \(R\) – сопротивление электроприбора в Омах. В электросеть включен предохранитель, который плавится, если сила тока превышает \(2{,}5\) А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.
\(\boxed{11}\) Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 96 литров она заполняет на 4 минуты быстрее, чем первая труба?
\(\boxed{12}\) Найдите наименьшее значение функции \(y=6\cos x+\dfrac{24}{\pi}x+5\) на отрезке \( \Big[-\dfrac{2\pi}{3};0\Big]\).
\(\boxed{13}\) a) Решите уравнение \( \dfrac{2\cos^2x-2\cos x \cos2x-1}{\sqrt{\sin x}}=0\).
б) Найдите все корни этого уравнения, пранадлежащие отрезку \(\Big[\dfrac{3\pi}{2};3\pi\Big] \).
\(\boxed{15}\) Решите неравенство \( 15^x-9\cdot 5^x-3^x+9\leqslant 0\).
Набор скрепок стоит 60 рублей. Какое наибольшее количество таких наборов можно будет купить на 850 рублей после понижения цены на 25%?
На диаграмме показана среднемесячная температура воздуха в городе N за каждый месяц некоторого года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме, сколько за этот год было месяцев с положительной среднемесячной температурой.
Найдите (в см\(^2\)) площадь \(S\) кольца, изображённого на клетчатой бумаге с размером клетки 2 см × 2 см (см. рис.). В ответе запишите \(\dfrac{S}{\pi}\).
Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется положительным. У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,8. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,02. Известно, что 76% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.
Найдите корень уравнения \(\log_{81}3^{2x-3}=3\).
Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса \(23\sqrt3\).
На рисунке изображен график \(y=f'(x)\) – производной функции \(f(x)\), определенной на интервале \((-15;5)\). Найдите количество точек максимума функции \(f(x)\) принадлежащих отрезку \([-12;3]\)
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 9. Найдите объем пирамиды.
Найдите значение выражения \(\left(\dfrac{7^{\frac12}\cdot 7^{\frac13}}{\sqrt[6]{7}}\right)^3\)
Сила тока в цепи \(I\) (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: \(I=\dfrac{U}{R}\), где \(U\) – напряжение в вольтах, \(R\) – сопротивление электроприбора в Омах. В электросеть включен предохранитель, который плавится, если сила тока превышает \(2{,}5\) А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.
Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 96 литров она заполняет на 4 минуты быстрее, чем первая труба?
a) Решите уравнение \( \dfrac{2\cos^2x-2\cos x \cos2x-1}{\sqrt{\sin x}}=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{3\pi}{2};3\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 3π/2 | 18. 5π/3 | 19. 7π/4 | 20. 11π/6 |
| 21. 2π | 22. 13π/6 | 23. 9π/4 | 24. 7π/3 |
| 25. 5π/2 | 26. 8π/3 | 27. 11π/4 | 28. 17π/6 |
| 29. 3π |
Решите неравенство \( 15^x-9\cdot 5^x-3^x+9\leqslant 0\).