Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ 17.18 (1-12;18)
Разбор варианта
\( \boxed{1}\) При оплате услуг через платежный терминал взимается комиссия 8%. Терминал принимает суммы, кратные 10 рублям. Ибрагим хочет положить на счет своего мобильного телефона не меньше 400 рублей. Какую минимальную сумму он должен внести в данный терминал?
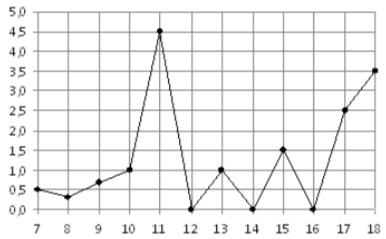
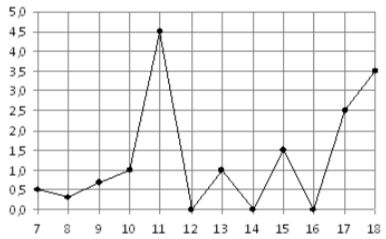
\( \boxed{2}\) На рисунке жирными точками показано суточное количество осадков, выпадавших в некотором городе с 7 по 18 декабря 2016 года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней за данный период не выпадало осадков.
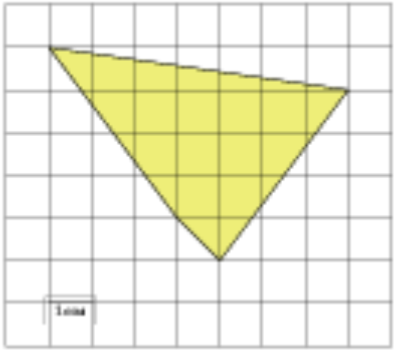
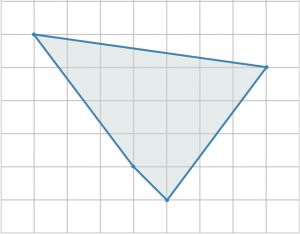
\( \boxed{3}\) Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
\( \boxed{4}\) Чтобы поступить в институт на специальность «Алхимик», абитуриент должен набрать на ЕГЭ не менее 62 баллов по каждому из трёх предметов – математика, латынь и химия. Чтобы поступить на специальность «Астролог», нужно набрать не менее 62 баллов по каждому из трёх предметов – математика, латынь и астрономия.
Вероятность того, что абитуриент А. получит не менее 62 баллов по математике, равна 0,4, по латыни – 0,6, по химии – 0,9 и по астрономии – 0,7.
Найдите вероятность того, что А. сможет поступить хотя бы на одну из двух упомянутых специальностей.
\( \boxed{5}\) Решите уравнение \( \log_7(16-2x)=2\log_7{3} \).
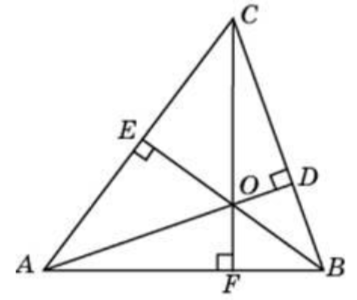
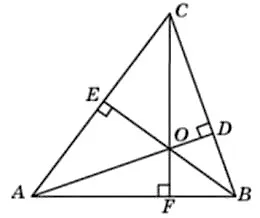
\( \boxed{6}\) В треугольнике \(ABC\) угол \(A\) равен 37°, угол \(B\) равен 68°. \(AD\), \(BE\) и \(CF\) - высоты, пересекающиеся в точке \(O\). Найдите угол \(AOF\). Ответ дайте в градусах.
\( \boxed{7}\) Материальная точка движется прямолинейно по закону \( x(t)=-\dfrac14 t^4+t^3+6t^2+7t+24 \), где \(x\) - расстояние от точки отсчета в метрах, \(t\) - время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени \(t=4\)c.
\( \boxed{8}\) Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в \(2{,}5\) раза?
\( \boxed{9}\) Найдите значение выражения \( 23\mathrm{tg\,}27°\cdot \mathrm{tg\,}63° \).
\( \boxed{10}\) Для определения эффективной температуры звезд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела \( P\), измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвертой степени температуры: \(P=\sigma ST^4 \), где \(\sigma=5{,}7\cdot 10^{-8} \) - постоянная, плозадь \(S\) измеряется в квадратных метрах, а температура \(T\) - в градусах Кельвина. Известно, что площадь поверхности некоторой звезды равна \( S=\dfrac1{81}\cdot 10^{21}\, м^2\), а излучаемая ею мощность \(P\) равна \( 9{,}12\cdot 10^{26}\) Вт. Найдите температуру этой звезды в градусах Кельвина.
\( \boxed{11}\) Смешали некоторое количество 14-процентного раствора некоторого вещества с таким же количеством 20-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
\( \boxed{12}\) Найдите точку минимума функции \( y=\dfrac43x\sqrt{x}-3x+91 \).
\( \boxed{18}\) Найдите все значения параметра \( a\), при которых неравенство \( 225^x-2(a-3)15^x+2a+2<0 \) не имеет решений.
При оплате услуг через платёжный терминал взимается комиссия 8%. Терминал принимает суммы, кратные 10 рублям. Ибрагим хочет положить на счет своего мобильного телефона не меньше 400 рублей. Какую минимальную сумму он должен внести в данный терминал?
На рисунке жирными точками показано суточное количество осадков, выпадавших в некотором городе с 7 по 18 декабря 2016 года. По горизонтали указываются числа месяца, по вертикали – количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней за данный период не выпадало осадков.
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Чтобы поступить в институт на специальность «Алхимик», абитуриент должен набрать на ЕГЭ не менее 62 баллов по каждому из трёх предметов – математика, латынь и химия. Чтобы поступить на специальность «Астролог», нужно набрать не менее 62 баллов по каждому из трёх предметов – математика, латынь и астрономия.
Вероятность того, что абитуриент А. получит не менее 62 баллов по математике, равна 0,4, по латыни – 0,6, по химии – 0,9 и по астрономии – 0,7.
Найдите вероятность того, что А. сможет поступить хотя бы на одну из двух упомянутых специальностей.
Решите уравнение \( \log_7(16-2x)=2\log_7{3} \).
В треугольнике ABC угол A равен 37°, угол B равен 68°. AD, BE и CF - высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
Материальная точка движется прямолинейно по закону \( x(t)=-\dfrac14 t^4+t^3+6t^2+7t+24 \), где \(x\) - расстояние от точки отсчета в метрах, \(t\) - время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени \(t=4\)c.
Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2,5 раза?
Найдите значение выражения \( 23\mathrm{tg\,}27°\cdot \mathrm{tg\,}63°\)
Для определения эффективной температуры звезд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела \( P\), измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвертой степени температуры: \(P=\sigma ST^4 \), где \(\sigma=5{,}7\cdot 10^{-8} \) - постоянная, площадь \(S\) измеряется в квадратных метрах, а температура \(T\) - в градусах Кельвина. Известно, что площадь поверхности некоторой звезды равна \( S=\dfrac1{81}\cdot 10^{21}\, м^2\), а излучаемая ею мощность \(P\) равна \( 9{,}12\cdot 10^{26}\) Вт. Найдите температуру этой звезды в градусах Кельвина.
Смешали некоторое количество 14-процентного раствора некоторого вещества с таким же количеством 20-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Найдите точку минимума функции \(y=\dfrac43x\sqrt{x}-3x+91\)
Найдите все значения параметра \( a\), при которых неравенство \( 225^x-2(a-3)15^x+2a+2<0 \) не имеет решений.