Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ 25.18 (1-19)
Разбор варианта
Тест по задачам можно пройти внизу страницы. Для прохождения надо авторизоваться на сайте. Результаты появятся в ЛК в разделе "Мои тесты".
\(\boxed{1}\) Держатели дисконтной карты книжного магазина получают при покупке скидку 10%. Книга стоит 130 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
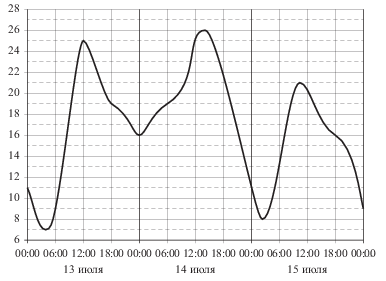
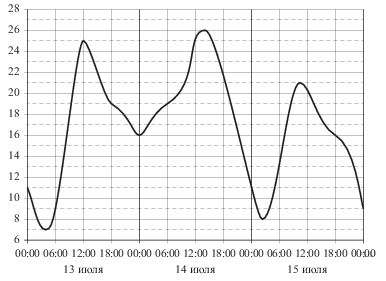
\(\boxed{2}\) На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 13 июля. Ответ дайте в градусах Цельсия.
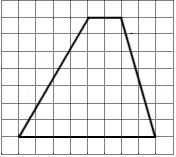
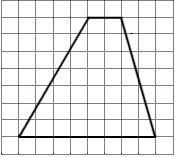
\(\boxed{3}\) На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину средней линии этой трапеции.
\(\boxed{4}\) В сборнике билетов по биологии всего 45 билетов, в 9 из них встречается вопрос по теме "Зоология". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме "Зоология".
\(\boxed{5}\) Найдите корень уравнения \((x-9)^3=27\).
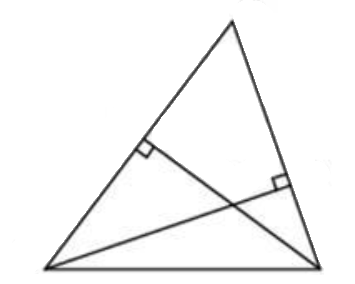
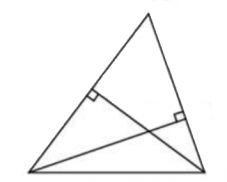
\(\boxed{6}\) Две стороны треугольника равны 24 и 26. Высота, опущенная на большую из этих сторон, равна 12. Найдите высоту, опущенную на меньшую из этих сторон треугольника.
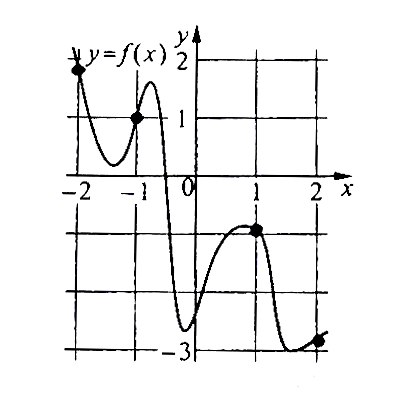
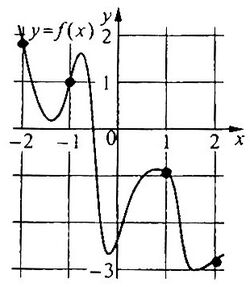
\(\boxed{7}\) На рисунке изображен график функции \(y=f(x)\). На оси абсцисс отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
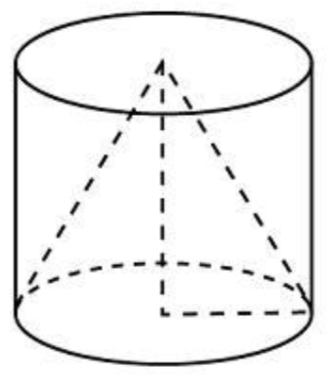
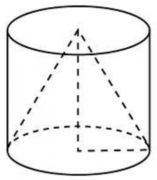
\(\boxed{8}\) Цилиндр и конус имеют общее основание и высоту. Объем конуса равен 3. Найдите объем цилиндра.
\(\boxed{9}\) Найдите значение выражения \( 2\cos2\alpha\), если \(\cos \alpha=0{,}7\).
\(\boxed{10}\) В ходе распада радиоактивного изотопа его масса уменьшается по закону \(m=m_0\cdot 2^{-\dfrac{t}{T}}\), где \(m_0\) – начальная масса изотопа, \(t\) – время, прошедшее от начального момента, \(T\) – период полураспада. В начальный момент времени масса изотопа \(20\; мг\). Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.
\(\boxed{11}\) Моторная лодка прошла против течения реки 72 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 9 км/ч. Ответ дайте в км/ч.
\(\boxed{12}\) Найдите точку минимума функции \(y=2x-2\ln(x-4)+10\).
\(\boxed{13}\) а) Решите уравнение \( 9^{\sin x}+9^{\sin(x+\pi)}=\dfrac{10}{3} \).
б) Укажите корни этого уравнения, принадлежащие отрезку \(\Big[ -\dfrac{7\pi}{2};-2\pi\Big]\).
\(\boxed{14}\) В пирамиде \(ABCD\) ребра \(DA\), \(DB\) и \(DC\) попарно перпендикулярны, а \(AB=BC=AC=7\sqrt2\).
а) Докажите, что эта пирамида правильная.
б) На ребрах \(DA\) и \(DC\) отмечены точки \(M\) и \(N\) соответственно, причем \(DM:MA=DN:NC=4:3\). Найдите площадь сечения \(MNB\).
\(\boxed{15}\) Решите неравенство \(1+\dfrac{4}{\log_5{x}-2}+\dfrac3{\log^2_5{x}-\log_5(5x^4)+5}\geqslant 0\).
\(\boxed{16}\) В равнобедренной трапеции \(ABCD\) основание \(AD\) в три раза больше основания \(BC\).
а) Докажите, что высота \(CH\) трапеции разбивает основание \(AD\) на отрезки, один из которых вдвое больше другого.
б) Найдите расстояние от вершины \(C\) до середины диагонали \(BD\), если \(AD=36\) и \(AC=26\).
\(\boxed{17}\) В июле 2020 года планируется взять кредит в банке на сумму \(185 640\) рублей.
Условия возврата таковы:
– каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть, за четыре года)?
\(\boxed{18}\) Найдите все значения параметра \(a\), при каждом из которых уравнение \( (3x-1)\ln(3x+a)=(3x-1)\ln(4x-a)\) имеет ровно один корень на отрезке \([0;1]\).
\(\boxed{19}\) Маша и Наташа делали фотографии несколько дней подряд. В первый день Маша сделала \(m\) фотографий, а Наташа — \(n\) фотографий. В каждый следующий день каждая из девочек делала на одну фотографию больше, чем в предыдущий день. Известно, что Наташа за всё время сделала суммарно на 1615 фотографии больше, чем Маша, и что фотографировали они больше одного дня.
а) Могли ли они фотографировать в течение 5 дней?
б) Могли ли они фотографировать в течение 6 дней?
в) Какое наибольшее суммарное число фотографий могла сделать Наташа за все дни фотографирования, если известно, что в последний день Маша сделала меньше 30 фотографий?
Держатели дисконтной карты книжного магазина получают при покупке скидку 10%. Книга стоит 130 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 13 июля. Ответ дайте в градусах Цельсия.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину средней линии этой трапеции.
В сборнике билетов по биологии всего 45 билетов, в 9 из них встречается вопрос по теме "Зоология". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме "Зоология".
Найдите корень уравнения \((x-9)^3=27\).
Две стороны треугольника равны 24 и 26. Высота, опущенная на большую из этих сторон, равна 12. Найдите высоту, опущенную на меньшую из этих сторон треугольника.
На рисунке изображен график функции \(y=f(x)\). На оси абсцисс отмечены точки -2, -1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Цилиндр и конус имеют общее основание и высоту. Объем конуса равен 3. Найдите объем цилиндра.
Найдите значение выражения \( 2\cos2\alpha\), если \(\cos \alpha=0{,}7\).
В ходе распада радиоактивного изотопа его масса \(m\) (в мг) уменьшается по закону \(m=m_0\cdot 2^{-\frac{t}{T}}\), где \(m_0\) – начальная масса изотопа, \(t\) – время (в минутах), прошедшее от начального момента, \(T\) – период полураспада (в минутах). В начальный момент времени масса изотопа 20 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.
Моторная лодка прошла против течения реки 72 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 9 км/ч. Ответ дайте в км/ч.
Найдите точку минимума функции \(y=2x-2\ln(x-4)+10\).
а) Решите уравнение \(9^{\sin x}+9^{\sin(x+\pi)}=\dfrac{10}{3}\)
б) Укажите корни этого уравнения, принадлежащие отрезку \(\left[ -\dfrac{7\pi}{2};-2\pi\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
a)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17.-7π/2 | 18. -10π/3 | 19. -13π/4 | 20. -19π/6 |
| 21. -3π | 22. -17π/6 | 23. -11π/4 | 24. -8π/3 |
| 25.-5π/2 | 26. -7π/3 | 27. -9π/4 | 28. -13π/6 |
| 29. -2π |
В пирамиде \(ABCD\) ребра \(DA\), \(DB\) и \(DC\) попарно перпендикулярны, а \(AB=BC=AC=7\sqrt2\).
а) Докажите, что эта пирамида правильная.
б) На ребрах \(DA\) и \(DC\) отмечены точки \(M\) и \(N\) соответственно, причем \(DM:MA=DN:NC=4:3\). Найдите площадь сечения \(MNB\).
Решите неравенство \(1+\dfrac{4}{\log_5{x}-2}+\dfrac3{\log^2_5{x}-\log_5(5x^4)+5}\geqslant 0\)
В равнобедренной трапеции ABCD основание AD в три раза больше основания BC.
а) Докажите, что высота CH трапеции разбивает основание AD на отрезки, один из которых вдвое больше другого.
б) Найдите расстояние от вершины C до середины диагонали BD, если AD=36 и AC=26.
В июле 2020 года планируется взять кредит в банке на сумму 185640 рублей. Условия возврата таковы:
– каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть, за четыре года)?
Найдите все значения параметра \(a\), при каждом из которых уравнение \( (3x-1)\ln(3x+a)=(3x-1)\ln(4x-a)\) имеет ровно один корень на отрезке \([0;1]\).
Маша и Наташа делали фотографии несколько дней подряд. В первый день Маша сделала \(m\) фотографий, а Наташа — \(n\) фотографий. В каждый следующий день каждая из девочек делала на одну фотографию больше, чем в предыдущий день. Известно, что Наташа за всё время сделала суммарно на 1615 фотографии больше, чем Маша, и что фотографировали они больше одного дня.
а) Могли ли они фотографировать в течение 5 дней?
б) Могли ли они фотографировать в течение 6 дней?
в) Какое наибольшее суммарное число фотографий могла сделать Наташа за все дни фотографирования, если известно, что в последний день Маша сделала меньше 30 фотографий?
Введите ответ в форме строки "да;да;1234". Где ответы на пунктыразделены ";", ипервые два ответа с маленькой буквы.