Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ 21.18 (1-12; 15)
Разбор варианта
\( \boxed{1}\) Одного рулона обоев хватает для оклейки полосы от пола до потолка шириной 1,2 м. Сколько рулонов обоев нужно купить для оклейки прямоугольной комнаты размерами 3,3 м на 4,2 м?
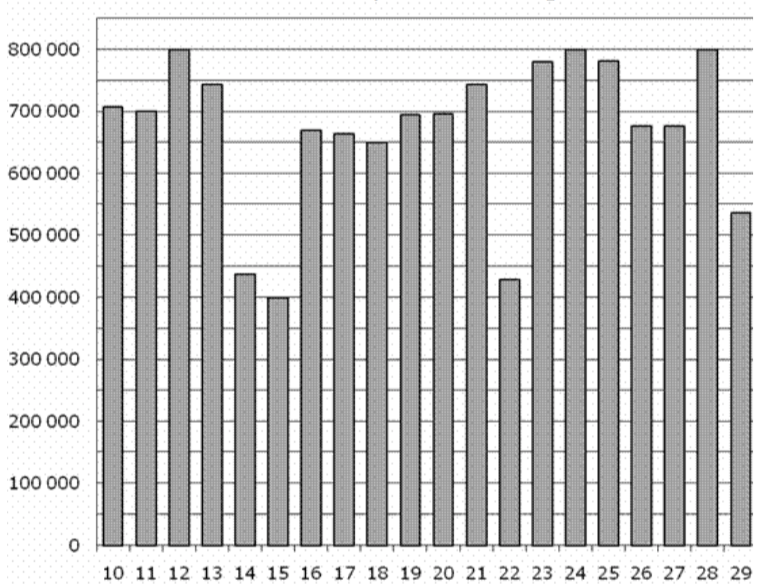
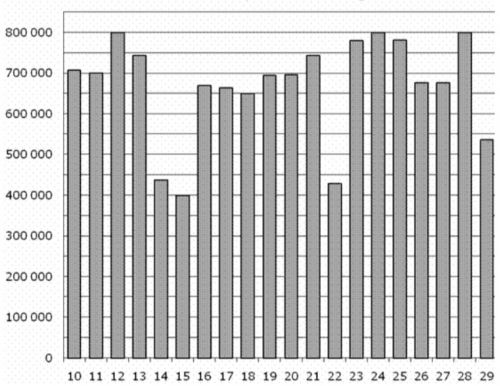
\( \boxed{2}\) На диаграмме показано количество посетителей сайта во все дни с 10 по 29 апреля 2011 года. По горизонтали указываются дни месяца, по вертикали – количество посетителей сайта за данный день. Найдите по диаграмме разницу между наибольшим и наименьшим суточным количеством посетителей данного сайта за указанный период.
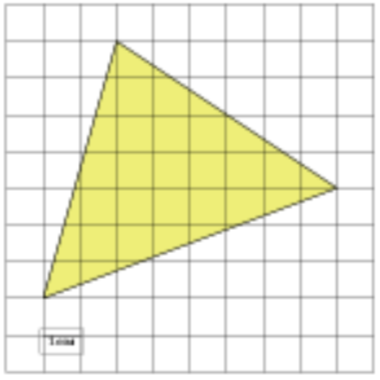
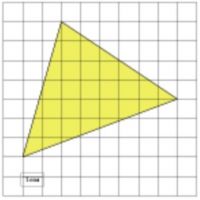
\( \boxed{3}\) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
\( \boxed{4}\) Помещение освещается двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,21. Найдите вероятность того, что в течение года не перегорит хотя бы одна лампа.
\( \boxed{5}\) Найдите наибольший отрицательный корень уравнения \( \sin\dfrac{(1-5x)\pi}{4}=\cos\left(-\dfrac{\pi}4\right) \).
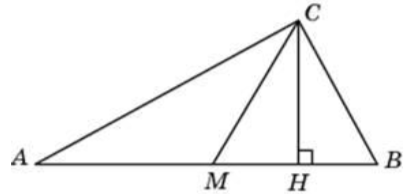
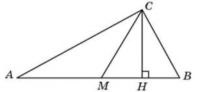
\( \boxed{6}\) Острые углы прямоугольного треугольника равны 56° и 34°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
\( \boxed{7}\) Прямая \(y=-4x+15\) является касательной к грайику функции \(y=x^3-6x^2+2x+7\). Найдите абсциссу точки касания.
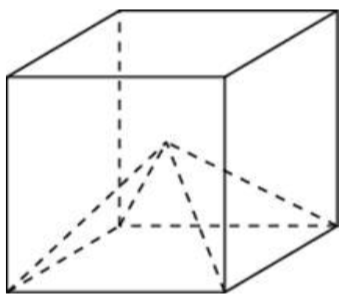
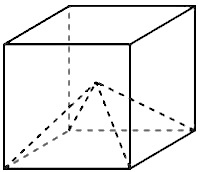
\( \boxed{8}\) Объем куба равен 42. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной – центр куба.
\( \boxed{9}\) Найдите значение выражения \( \dfrac{x^{4{,}14}\cdot x^{1{,}77}}{x^{3{,}94}} \) при \( x=\dfrac{7}{10} \).
\( \boxed{10}\) По закону Ома для полной цепи сила тока, измеряемая в амперах, равна \(I=\dfrac{\varepsilon}{R+r}\), где \(\varepsilon \) – ЭДС источника (в Вольтах), \(r=3\) Ом – его внутреннее сопротивление, \(R\) – сопротивление цепи (в Омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 25% от силы тока короткого замыкания \( I_{кз}=\dfrac{\varepsilon}{r}\)? Ответ выразите в Омах.
\( \boxed{11}\) Аристарху надо решить 140 задач. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Аристарх решил 8 задач. Определите, сколько задач решил Аристарх в последний день, если со всеми задачами он справился за 7 дней.
\( \boxed{12}\) Найдите наименьшее значение функции \(y=x^{\frac32}-18x+25\) на отрезке \( [7;295]\).
\( \boxed{15}\) Решите неравенство \( 25^x+5^{x+1}+5^{1-x}+\dfrac1{25^x}\leqslant 12 \)
Ответы
1) 13
2) 400000
3) 25
4) 0,9559
5) -0,4
6) 22
7) 2
8) 7
9) 0,49
10) 9
11) 32
12) -839
12) 0
Одного рулона обоев хватает для оклейки полосы от пола до потолка шириной 1,2 м. Сколько рулонов обоев нужно купить для оклейки прямоугольной комнаты размерами 3,3 м на 4,2 м?
На диаграмме показано количество посетителей сайта во все дни с 10 по 29 апреля 2011 года. По горизонтали указываются дни месяца, по вертикали – количество посетителей сайта за данный день. Найдите по диаграмме разницу между наибольшим и наименьшим суточным количеством посетителей данного сайта за указанный период.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Помещение освещается двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,21. Найдите вероятность того, что в течение года не перегорит хотя бы одна лампа.
Найдите наибольший отрицательный корень уравнения \( \sin\dfrac{(1-5x)\pi}{4}=\cos\left(-\dfrac{\pi}4\right) \)
Острые углы прямоугольного треугольника равны 56° и 34°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Прямая \(y=-4x+15\) является касательной к графику функции \(y=x^3-6x^2+8x+7\). Найдите абсциссу точки касания.
Объем куба равен 42. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной – центр куба.
Найдите значение выражения \( \dfrac{x^{4{,}17}\cdot x^{1{,}77}}{x^{3{,}94}} \) при \( x=\dfrac{7}{10} \).
По закону Ома для полной цепи сила тока, измеряемая в амперах, равна \(I=\dfrac{\varepsilon}{R+r}\), где \(\varepsilon \) – ЭДС источника (в Вольтах), \(r=3\) Ом – его внутреннее сопротивление, \(R\) – сопротивление цепи (в Омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 25% от силы тока короткого замыкания \( I_{кз}=\dfrac{\varepsilon}{r}\)? Ответ выразите в Омах.
Аристарху надо решить 140 задач. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Аристарх решил 8 задач. Определите, сколько задач решил Аристарх в последний день, если со всеми задачами он справился за 7 дней.
Найдите наименьшее значение функции \(y=x^{\frac32}-18x+25\) на отрезке \( [7;295]\).
Решите неравенство \( 25^x+5^{x+1}+5^{1-x}+\dfrac1{25^x}\leqslant 12 \).