Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ профиль 4.19
Показания счетчика электроэнергии 1 мая составляли 36364 кВт·ч, а 1 июня — 36544 кВт·ч. Сколько нужно заплатить за электроэнергию за май, если 1 кВт·ч стоит 2 рубля 50 копеек? Ответ дайте в рублях.
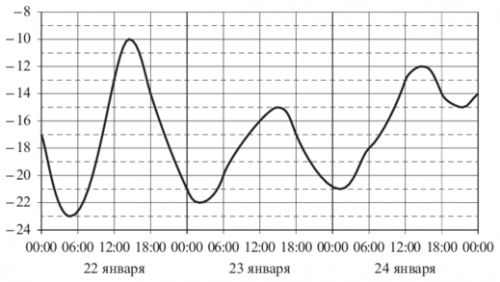
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указываются дата и время, по вертикали — значения температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 24 января. Ответ дайте в градусах Цельсия.
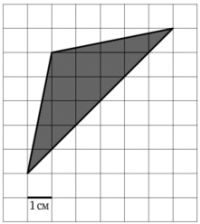
На клетчатой бумаге с размером клетки \(1\times1\) изображен треугольник. найдите его площадь.
Девять детей встают в хоровод в случайном порядке. Среди них Артур и его брат Марк. Какова вероятность, что Артур и Марк окажутся рядом?
Решите уравнение \( \log_{\pi}(3-2x)=2\log_{\pi}x\). Если корней несколько, в ответ напишите меньший из них.
В треугольнике ABC стороны AC и BC равны, высота AH равна 7, BH=24. Найдите синус угла BAC.
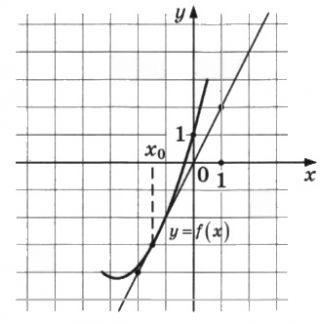
На рисунке изображены график функции \(y=f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).
Во сколько раз увеличится площадь поверхности куба, если все его ребра увеличить в 4 раза?
Вычислите \(\log_2\log_2\log_2{16^{64}}\).
Мяч бросили под углом \(\alpha\) к плоской горизонтальной поверхности земли. Время полета мяча (в секундах) определяется по формуле \(t=\dfrac{2v_0\sin\alpha}{g}\). При каком значении угла \(\alpha\) (в градусах) время полета составит 2,6 секунды, если мяч бросают с начальной скоростью \(v_0=13\, м/с\)? Считайте, что ускорение свободного падения \(g=10\, м/с^2\)
Имеется два сосуда. Первый содержит 100 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 67% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 77% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Найдите точку минимума функции \(y=(10-x)e^{10-x}\).
а) Решите уравнение \((1-3\mathrm{tg\,}^2x)\sqrt{13\sin x}=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-2\pi;-\dfrac{\pi}2\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -2π | 18. -11π/6 | 19. -7π/4 | 20. -5π/3 |
| 21. -3π/2 | 22. -4π/3 | 23. -5π/4 | 24. -7π/6 |
| 25. -π | 26. -5π/6 | 27. -3π/4 | 28. -2π/3 |
| 29. -π/2 |
В правильной четырехугольной призме \(ABCDA_1B_1C_1D_1\) сторона основания\(AB\) равна 5, а боковое ребро равно \(\sqrt5\). На ребрах \(BC\) и \(C_1D_1\) отмечены точки \(K\) и \(L\) соответственно, причем \(CK=2\), а \(C_1L=1\). Плоскость \(\alpha\) параллельна прямой \(BD\) и содержит точки \(K\) и \(L\).
а) Докажите, что прямая \(A_1C\) перпендикулярна плоскости \(\alpha\).
б) Найдите объем пирамиды, вершина которой — точка \(A_1\), а основание — сечение данной призмы плоскостью \(\alpha\).
Решите неравенство \(\log_{|x|}(15x-18-2x^2)\leqslant 2\).
Точка O — центр описанной около треугольника ABC окружности, точка I — центр вписанной в этот треугольник окружности, точка H — точка пересечения высот треугольника ABC. Известно, что ∠BAC=∠OBC+∠OCB.
а) Докажите, что точка I лежит на окружности, описанной около треугольника BOC.
б) Найдите угол OIH, если ∠ABC=75°
31 декабря 2014 года Альберт взял в банке кредит на сумму 5460000 рублей под 20% годовых. Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть, увеличивает долг на 20%), затем Альберт переводит в банк x рублей. Какой должна быть сумма x, чтобы Альберт выплатил долг тремя равными платежами (то есть за три года)?
Найдите все значения параметра \(a\), при которых уравнение \((4x-x^2)^2-32\sqrt{4x-x^2}=a^2-14a\) имеет хотя бы одно решение.
Выберите все промежутки, составляющие ответ.
На доске были написаны несколько целых чисел. Несколько раз с доски стирали по два числа, сумма которых делится на 3.
а) Может ли сумма всех оставшихся на доске чисел равняться 8, если сначала по одному разу были написаны числа 3, 4, 5, 6, 7, 8, 9, 10, 11, 12?
б) Может ли на доске остаться ровно два числа, разность между которыми равна 54, если сначала по одному разу были написаны все натуральные числа от 200 до 299 включительно?
в) Известно, что на доске осталось ровно два числа, а сначала были по одному разу написаны все натуральные числа от 200 до 299 включительно. Какое наибольшее значение может получиться, если поделить одно из оставшихся чисел на второе из них?
Введите ответ в форме строки "да;да;23:34", где ответы на пункты разделены ";", первые два ответа с маленькой буквы, а ответ на пункт в) в виде отношения, записанного через ":".