Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ профиль 2.20
Держатели дисконтной карты книжного магазина получают при покупке скидку 5%. Книга стоит 140 рублей. Сколько рублей заплатит держатель дисконтной карты за эту книгу?
На диаграмме показана среднемесячная температура воздуха во Владивостоке за каждый месяц 2013 г. По горизонтали указываются месяцы; по вертикали — температура в градусах Цельсия. Определите по приведённой диаграмме, сколько было месяцев с отрицательной среднемесячной температурой.
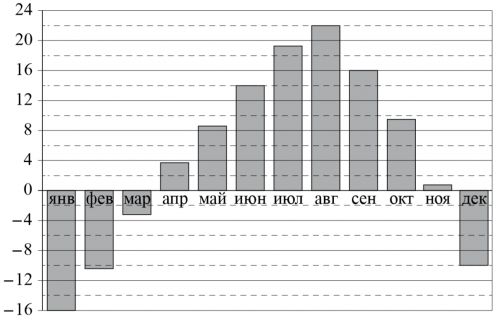
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите его площадь.
В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что сумма выпавших очков будет чётной.
Найдите корень уравнения \(\log_8(5x+47)=3\).
В треугольнике \(ABC\) угол \(C\) равен 90°, \(AB=40\), \(AC=4\sqrt{51}\). Найдите \(\sin A\).
На рисунке изображен график функции \(y=f(x)\), определенной на интервале (-1;13). Определите количество целых точек, в которых производная функции \(f(x)\) положительна.
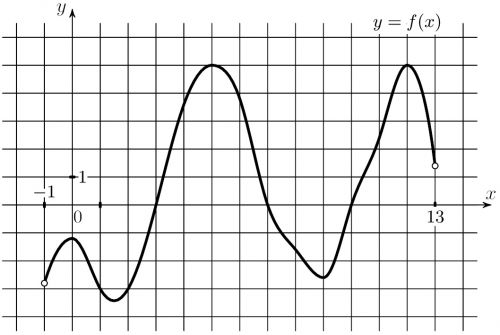
Найдите площадь поверхности многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
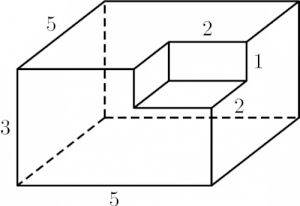
Найдите значение выражения \(4^{\frac15}\cdot 16^{\frac9{10}}\).
Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой \(\eta=\dfrac{T_1-T_2}{T_1}\cdot 100\%\), где \(T_1\) – температура нагревателя (в градусах Кельвина), \(T_2\) – температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя \(T_1\) КПД этого двигателя будет не меньше 50%, если температура холодильника \(T_2=250 K\)? Ответ дайте в кельвинах.
Два велосипедиста одновременно отправились в 224-километровый пробег. Первый ехал со скоростью, на 2 км/ч большей, чем скорость второго, и прибыл к финишу на 2 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Найдите наибольшее значение функции \(y=89x-87\sin x+31\) на отрезке \(\left[-\dfrac{\pi}{2};0\right]\).
а) Решите уравнение \(6\sin^2x-5\sin x-4=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[ -\dfrac{7\pi}{2};-\dfrac{3\pi}2\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
a)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17.-7π/2 | 18. -10π/3 | 19. -13π/4 | 20. -19π/6 |
| 21. -3π | 22. -17π/6 | 23. -11π/4 | 24. -8π/3 |
| 25.-5π/2 | 26. -7π/3 | 27. -9π/4 | 28. -13π/6 |
| 29. -2π | 30. -11π/6 | 31. -7π/4 | 32. -5π/3 |
Ребро SA пирамиды SABC перпендикулярно плоскости основания ABC.
а) Докажите, что плоскость, проходящая через середины рёбер AB, AC и SA, отсекает от пирамиды SABC пирамиду, объём которой в 8 раз меньше объёма пирамиды SABC.
б) Найдите расстояние от вершины A до этой плоскости, если SA=2√5, AB=AC=10, BC=4√5.
Решите неравенство \(\log^2_{|x|}(x^2)+\log_2(x^2)\leqslant 8\)
Сторона CD прямоугольника ABCD касается некоторой окружности в точке M. Продолжение стороны AD пересекает эту окружность в точках P и Q, причем точка P лежит между точками D и Q. Прямая BC касается окружности, а точка Q лежит на прямой BM.
а) Докажите, что ∠DMP=∠CBM.
б) Известно, что CM=17 и CD=25. Найдите сторону AD.
15-го января Егор взял кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что восьмая выплата составила 108 тысяч рублей. Сколько рублей Егор взял в кредит?
Найдите все значения параметра \(a\), при каждом из которых уравнение \(\left\vert\log_7(x^2)-a\right\vert-\left \vert \log_7x+2a\right \vert=(\log_7x)^2\) имеет ровно четыре решения.
В результате опроса выяснилось, что примерно 58% опрошенных предпочитают искусственную ёлку натуральной. Из этого же опроса последовало, что примерно 42% респондентов никогда не отмечали Новый год не дома. Эти результаты получились с помощью округления до целого числа.
а) Могло ли в опросе участвовать ровно 40 человек?
б) Могло ли в опросе участвовать ровно 48 человек?
в) Какое наименьшее количество человек могло участвовать в этом опросе?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.