Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ (условия)
1) В школе испанский язык изучает 171 учащийся, что составляет 36% от числа всех учащихся школы. Сколько учащихся в школе?
2) В городе N 150000 жителей. Срели них 15% детей и подростков. Среди взрослых 45% не работают. Сколько взрослых жителей работает?
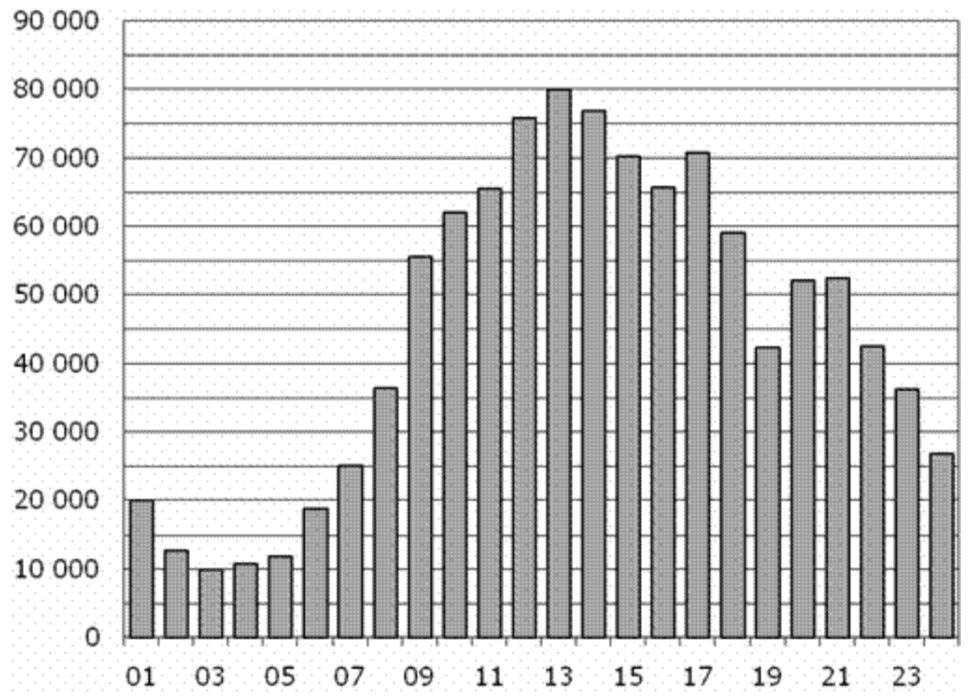
3) На диаграмме показано количество посетителей сайта в течение каждого часа 12 марта 2014 года. По горизонтали указывается час, по вертикали – количество посетителей сайта на протяжении этого часа. Определите по диаграмме, в течении какого часа на сайте побывало минимальное количество посетителей.
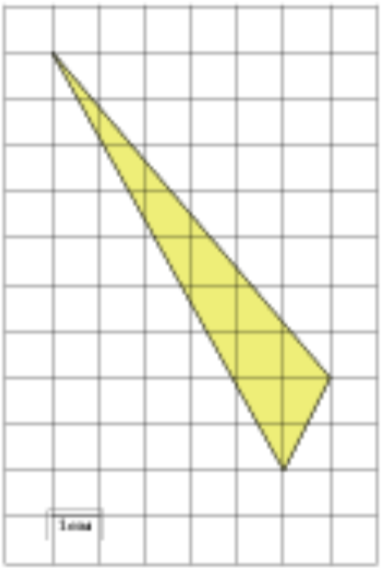
4) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
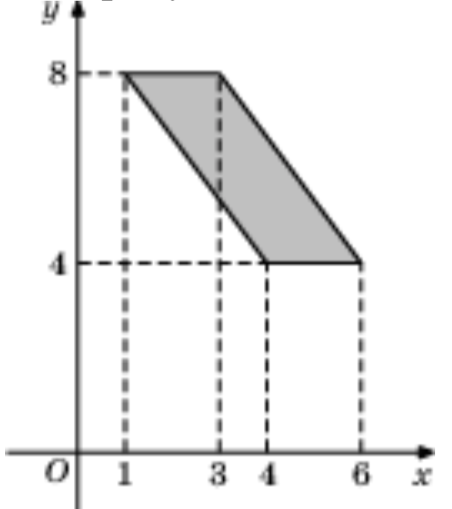
5) Найдите площадь параллелограмма, изображенного на рисунке.
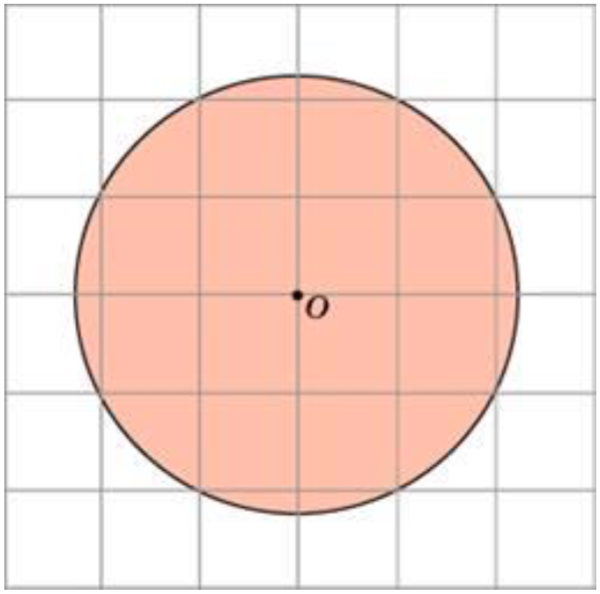
6) Найдите площадь \(S\) круга, считая стороны квадратных клеток равными 2. В ответе
укажите \( \dfrac{S}{\pi}\).
7) На клетчатой бумаге с размером клетки 1 × 1 изображён угол. Найдите его градусную величину.
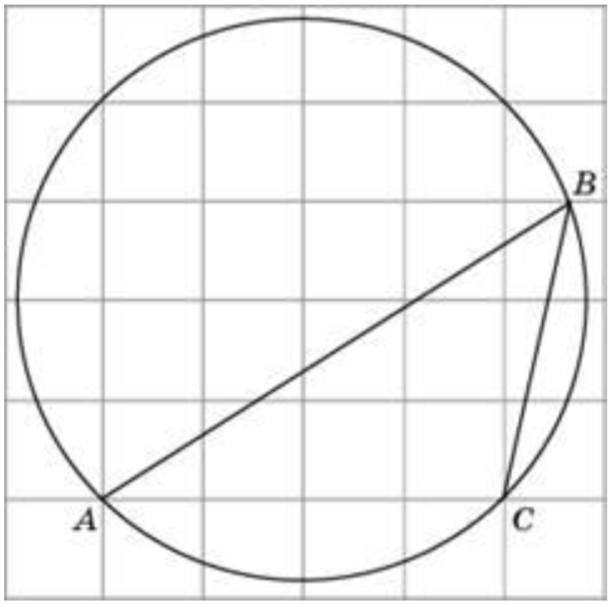
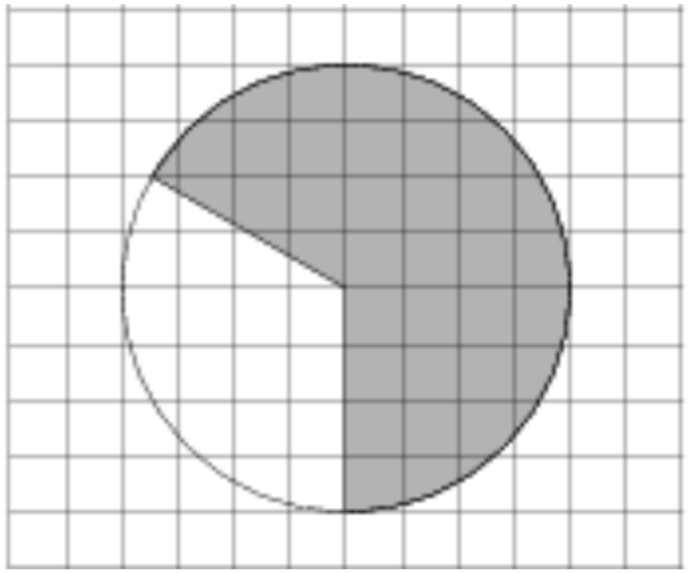
8) На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 12?
9) На чемпионате по стрельбе выступают 50 спортсменов, среди них 8 спортсменов из России и 5 прыгунов из Аргентины. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что тринадцатым будет выступать спортсмен из России.
10) На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Окружность», равна 0,15. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику не достанется вопрос ни по одной из этих двух тем.
11) Биатлонист 4 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что биатлонист первые 3 раза попал в мишени, а последний раз промахнулся.
12) На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной и больше 3?
13) В группе туристов 8 человек. С помощью жребия они выбирают двух человек, которые должны идти к реке за водой. Какова вероятность того, что турист А., входящий в состав группы, пойдёт за водой?
14) Ковбой Джон попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,4. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
15) На фабрике керамической посуды 20% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 90% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.
16) Найдите корень уравнения \(\sqrt{-72+17x}=x\). Если уравнение имеет более одного корня, укажите меньший из них.
17) Решите уравнение \(\left( \dfrac1{49}\right)^{x-8}=7\).
18) Найдите корень уравнения \(\dfrac{3x}{x^2-4}=1\). Если уравнение имеет более одного корня, укажите больший из них.
19) Решите уравнение \(\log_5(7-2x)=3\log_5{3}\).
20) Найдите наибольший отрицательный корень уравнения \(\sin{\dfrac{\pi(2x-3)}{6}}=\cos{-\dfrac{\pi}{6}}\).
21) Два угла треугольника равны 60° и 43°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
22) В треугольнике ABC угол C равен 90°, угол A равен 30°, AB= \(78 \sqrt3\). Найдите высоту CH.
23) Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его периметр.
24) Боковые стороны равнобедренного треугольника равны 109, основание равно 182. Найдите радиус вписанной окружности.
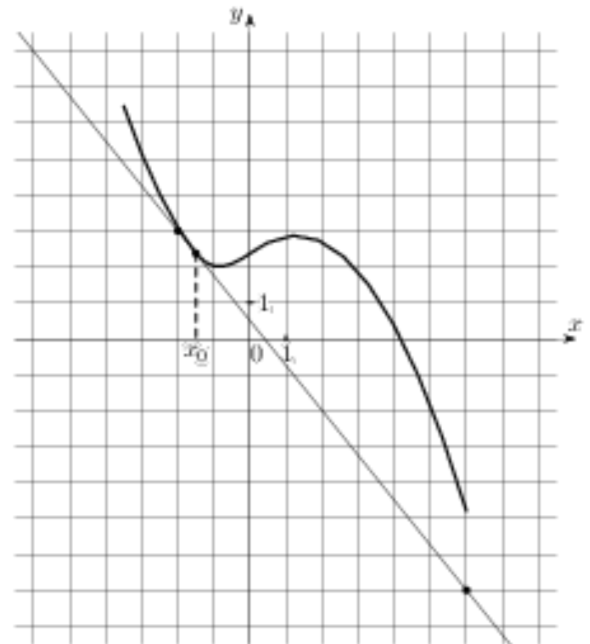
25) На рисунке изображены график функции \( y=f(x)\) и касательная к нему в точке с абсциссой \(x_0\). Найдите значение производной функции \(f(x)\) в точке \(x_0\).
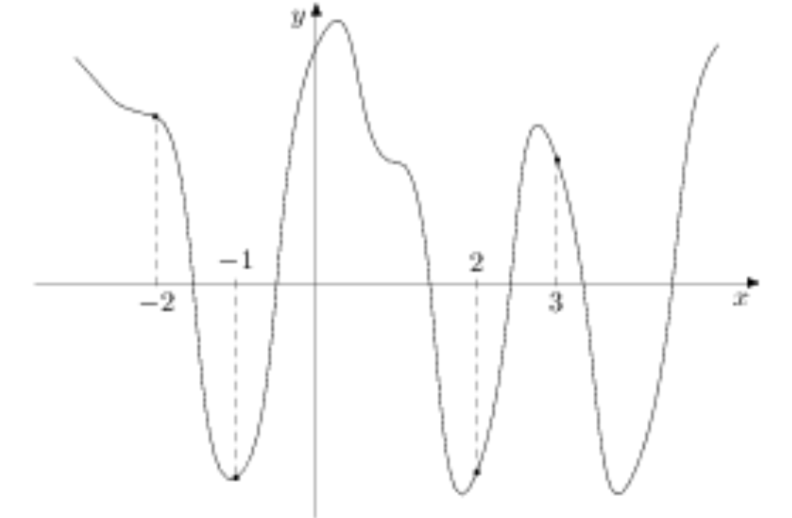
26) На рисунке изображён график функции \(y=f(x)\). На оси абсцисс отмечены точки −2, −1, 2, 3. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
27) Материальная точка движется прямолинейно по закону \( x(t)=\dfrac16 t^3 - 2t^2-4t+3\), где \(x\) – расстояние от точки отсчета в метрах, \(t\) – время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 38 м/с?
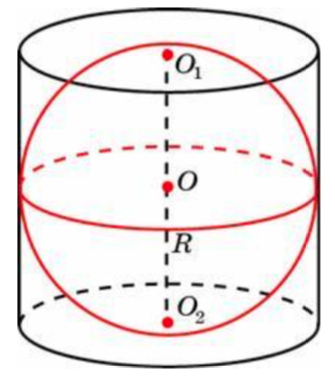
28) Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара.
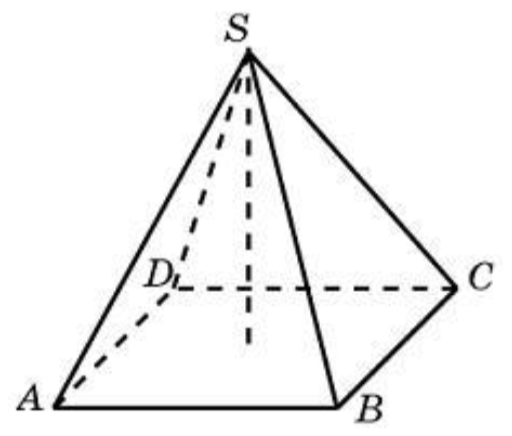
29) В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
30) Найдите объем многогранника, вершинами которого являются точки \( A, B, C, B_1\) правильной шестиугольной призмы \(ABCDEFA_1B_1C_1D_1E_1F_1\), площадь основания которой равна 6, а боковое ребро равно 3.
31) Найдите значение выражения \(\dfrac{30}{\cos^2 {48°}+\cos^2{138°}}\).
32) Найдите \(\sin{\alpha}\), если \(\cos{\alpha}=\dfrac{\sqrt{51}}{10}\) и \( \alpha \in \left( -\dfrac{\pi}{2}; 0\right) \).
33) Найдите значение выражения \( (1-\log_4{32})(1-\log_8{32})\).
34) При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу, частота звукового сигнала, регистрируемого приёмником, не совпадает с частотой исходного сигнала \(f_0= 110\) Гц и определяется следующим выражением: \(f=f_0\dfrac{c+u}{c-v}\) (Гц), где \(c\) − скорость распространения сигнала в среде (в м/с), а \(u = 9 \,м/с\) и \(v = 15 \,м/с\) − скорости приёмника и источника относительно среды соответственно. При какой максимальной скорости \(c\) (в м/с) распространения сигнала в среде частота сигнала в приёмнике \(f\) будет не менее 120 Гц?
35) Из городов A и B одновременно навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 4 часа раньше, чем велосипедист приехал в A, а встретились они через 50 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
36) Найдите точку минимума функции \(y=(x^2-31x+31)e^{15-x}\).
15) Решите неравенство \( \log_2(x-1)+\log_2\left(x^2+\dfrac1{x-1}\right)\leqslant 2\log_2\left( \dfrac{x^2+x-1}{2}\right) \).
15 января планируется взять кредит в банке на некоторую сумму на 21 месяц. Условия его возврата таковы:
- 1 числа каждого месяца долг увеличивается на 2% по сравнению с концом предыдущего месяца;
- со 2 по 14 число каждого месяца необходимо выплатить одним плетежом часть долга;
- на 15 число каждого с 1 по 20 месяц долг должен уменьшаться на 40 тыс. рублей;
- за 21 месяц долг должен быть погашен полностью.
Сколько тысяч рублей составляет долг на 15 число 20-го месяца, если банку всего было выплачено 1820 тыс. рублей?
18)При всех значениях параметра \(a\) найдите количество решений системы уравнений
\(\begin{cases} x^4+y^2=2a-7\\
x^2+y=|a-3|
\end{cases}\)