Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ профиль 9.19
Показания счётчика электроэнергии 1 февраля составляли 1428 кВт·ч, а 1 марта — 1728 кВт·ч. Сколько нужно заплатить за электроэнергию за февраль, если 1 кВт·ч электроэнергии стоит 1 рубль50 копеек? Ответ дайте в рублях.
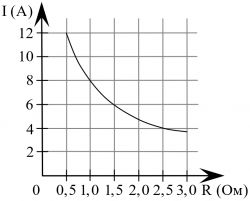
Мощность отопителя в автомобиле регулируется дополнительным сопротивлением, которое можно менять, поворачивая рукоятку в салоне машины. При этом меняется сила тока в электрической цепи электродвигателя — чем меньше сопротивление, тем больше сила тока, и тем быстрее вращается мотор отопителя. На рисунке показана зависимость силы тока от величины сопротивления. На оси абсцисс откладывается сопротивление (в омах), на оси ординат — сила тока в амперах. Сопротивление цепи увеличилось с 1 Ом до 2,5 Ом. На сколько ампер при этом уменьшился ток в цепи?
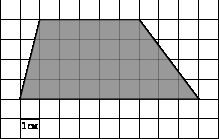
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Вымпел» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Вымпел» выиграет жребий ровно один раз.
Решите уравнение \(\sqrt{13-4x}=13\). Если корней несколько, в ответ запишите больший из них.
Четырехугольник ABCD вписан в окружность. Угол BAC равен 31°, угол ADB равен 20°. Найдите угол ABC. Ответ дайте в градусах.
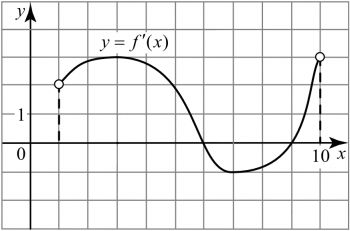
На рисунке изображён график функции \(y=f'(x)\) — производной функции \(y=f(x)\), определенной на интервале (1; 10). Найдите точку минимума функции \(f(x)\).
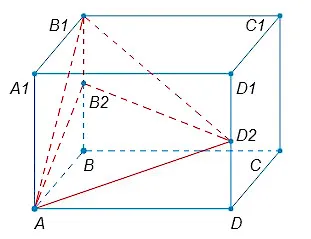
В прямоугольном параллелепипеде \(ABCDA_1B_1C_1D_1\) точки \(B_2\) и \(D_2\) — середины сторон \(BB_1\) и \(DD_1\) соответственно. Найдите объем многогранника \(D_2AB_2B_1\), если \(AD = 18\), \(AA_1 = 3\), \(A_1B_1 = 10\).
Найдите значение выражения \(\sqrt{48}\cos^2{\dfrac{7\pi}{12}}-\sqrt{12}\).
Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением \(p_1V_1^{1{,}4}=p_2V_2^{1{,}4}\), где \(p_1\) и \(p_2\) — давление газа (в атмосферах) в начальном и конечном состояниях, \(V_1\) и \(V_2\) — объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен 729 л, а давление газа равно \(\dfrac1{27}\) атмосферы. До какого объёма нужно сжать газ, чтобы давление в сосуде стало равно 81 атмосфере? Ответ дайте в литрах.
Имеется два сплава. Первый сплав содержит 5% меди, второй — 40% меди. Масса первого сплава больше массы второго на 50 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Найдите точку максимума функции \(y=2{,}5x^2-19x+18\ln x+17\)
а) Решите уравнение \(2\log^2_{0{,}5}(2\sin x)-7\log_2(2\sin x)+3=0\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-3\pi;-\dfrac{3\pi}2\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -3π | 18. -17π/6 | 19. -11π/4 | 20. -8π/3 |
| 21. -5π/2 | 22. -7π/3 | 23. -9π/4 | 24. -13π/6 |
| 25. -2π | 26. -11π/6 | 27. -7π/4 | 28. -5π/3 |
| 29. -3π/2 |
Дана пирамида \(SABC\), в которой \(SC=SB=\sqrt{17}\), \(AB=AC=\sqrt{29}\), \(SA=BC=2\sqrt{5}\)
а) Докажите, что ребро \(SA\) перпендикулярно ребру \(BC\).
б) Найдите угол между прямой \(SA\) и плоскостью \(SBC\).
Решите неравенство \(\dfrac{2^{5+x}-2^{-x}}{2^{3-x}-4^{-x}}\geqslant 2^x\)
Дана трапеция ABCD с основаниями BC и AD. Точки M и N являются серединами сторон AB и CD соответственно. Окружность, проходящая через точки B и С, пересекает отрезки BM и CN в точках P и Q (отличных от концов отрезков).
а) Докажите, что точки M, N, P и Q лежат на одной окружности.
б) Найдите QN, если отрезки DP и PC перпендикулярны, AB = 21, BC = 4, CD = 20, AD = 17
В июле 2019 года планируется взять кредит в банке на три года в размере S млн рублей, где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 30% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей
| Месяц и год | Июль 2019 | Июль 2020 | Июль 2021 | Июль 2022 |
| Долг (в млн руб.) | S | 0,7S | 0,3S | 0 |
Найдите наименьшее S, при котором каждая из выплат будет больше 3 млн руб.
Найдите все значения параметра \(a\), при которых наименьшее значение функции \(f(x)=x-2|x|+|x^2-2(a+1)x+a^2+2a|\) больше -4.
Вася и Петя решали задачи из сборника, и они оба решили все задачи этого сборника. Каждый день Вася решал на одну задачу больше, чем в предыдущий день, а Петя решал на две задачи больше, чем в предыдущий день. Они начали решать задачи в один день, при этом в первый день каждый из них решил хотя бы одну задачу.
а) Могло ли получиться так, что Вася в первый день решил на одну задачу меньше, чем Петя, а Петя решил все задачи из сборника ровно за 5 дней?
б) Могло ли получиться так, что Вася в первый день решил на одну задачу больше, чем Петя, а Петя решил все задачи из сборника ровно за 4 дня?
в) Какое наименьшее количество задач могло быть в сборнике если каждый из ребят решал задачи более 6 дней, причем в первый день один из мальчиков решил на одну задачу больше чем другой?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.