Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ профиль 3.19
Магазин делает пенсионерам скидку на определенное количество процентов от цены покупки. Пакет молока стоит в магазине 75 рублей. Пенсионер заплатил за него 72 рубля. Сколько процентов составляет скидка для пенсионеров?
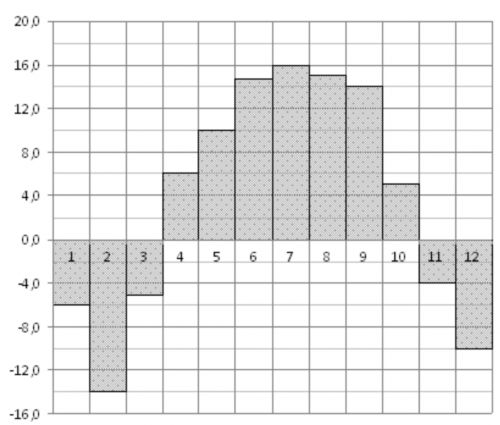
На диаграмме показана среднемесячная температура в городе N за каждый месяц некоторого года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме разность наибольшей и наименьшей среднемесячных температур в зимние месяцы этого года.
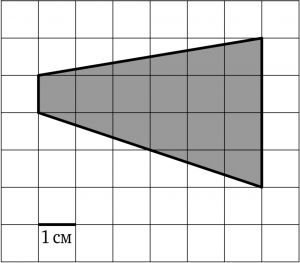
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки \(1\, см\times 1\, см\). Ответ дайте в квадратных сантиметрах.
Мирон, Святополк, Любава, Нэлли, Платон, Ангелина, Рудольф и Серёжа бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.
Решите уравнение \(\left( \dfrac19\right)^{2+x}=729\).
Площадь параллелограмма ABCD равна 68. Точка E середина стороны BC. Найдите площадь четырехугольника AECD.
Найдите абсциссу точки касания прямой прямой \(y=-6x-10\) и графика функции \(y=x^3+4x^2-6x-10\).
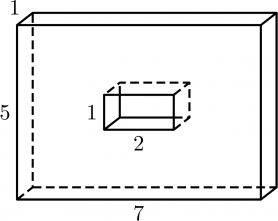
Найдите площадь поверхности многогранника, изображенного на рисунке. Все двугранные углы прямые.
Найдите значение выражения \(\left( \sqrt{2\dfrac{4}{7}}-\sqrt{7\dfrac{1}{7}}\right):\sqrt{\dfrac{2}{63}}\).
Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой \(m_В\) (в килограммах) от температуры \(t_1\) до температуры \(t_2\) (в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы \(m_{др}\) кг. Он определяется формулой \(\nu=\dfrac{c_В\cdot m_В(t_2-t_1)}{q_{др}\cdot m_{др}}\cdot 100\%\), где \(c_В=4{,}2\cdot10^3Дж/(кг\cdotК)\) – теплоёмкость воды, \(q_{др}=8{,}3\cdot10^6Дж/кг\) – удельная теплота сгорания дров. Определите наименьшее количество дров, которое понадобится сжечь в кормозапарнике, чтобы нагреть \(m_В = 166\, кг\) воды от 10°C до кипения, если известно, что КПД кормозапарника не больше 14%. Ответ выразите в килограммах.
Моторная лодка прошла против течения реки 99 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 1 км/ч. Ответ дайте в км/ч.
Найдите наибольшее значение функции \(y=93x-89\sin x+31\) на отрезке \(\left[ -\dfrac{\pi}{2};0\right]\).
a) Решите уравнение \(169^{\cos^2x}=13^{\sqrt2\cos x}\)
б) Найдите все корни этого уравнения, принадлежащие отрезку [2π;3π].
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 2π | 18. 13π/6 | 19. 9π/4 | 20. 7π/3 |
| 21. 5π/2 | 22. 8π/3 | 23. 11π/4 | 24. 17π/6 |
| 25. 3π | 26. 11π/6 | 27. 7π/4 | 28. 5π/3 |
| 29. 3π/2 |
В основании прямой треугольной призмы \(ABCA_1B_1C_1\) лежит равнобедренный треугольник \(ABC\) с основанием \(AC\). Точка \(K\) - середина ребра \(A_1B_1\), а точка \(M\) делит ребро \(АС\) в отношении \(AM:MC=1:3\).
а) Докажите, что \(KM\) перпендикулярно \(AC\).
б) Найдите угол между прямой \(KM\) и плоскостью \(ABB_1\), если \(AB=5\), \(AC=8\) и \(AA_1=4\).
Решите неравенство \(\log_{2x}4+3\leqslant \log_2{8x}\)
На катетах ACи BC прямоугольного треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M – середина гипотенузы AB, Н – точка пересечения прямых CM и DK.
а) Докажите, что CM⊥DK.
б) Найдите MH, если катеты AC=3, BC=4.
По бизнес-плану предполагается вложить в четырёхлетний проект целое число млн рублей. По итогам каждого года планируется прирост средств вкладчика на 30% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 10 млн рублей в первый и второй годы, а также по 9 млн в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений (в млн руб.), при котором общая сумма средств вкладчика к началу третьего года станет больше 140 млн, а к концу проекта – больше 250 млн рублей.
Найдите все значения параметра \(a\), при котором система
\(\begin{cases}
(ay+ax+3)(y+x-a)=0\\
|xy|=a
\end{cases}\)
имеет от одного до пяти решений.
Пусть K(n) обозначает сумму квадратов всех цифр натурального числа n.
а) Существует ли такое трехзначное число n, что K(n)=181?
б) Существует ли такое трехзначное число n, что K(n)=180?
в) Какое наименьшее значение может принимать выражение 9K(n)-n, если n – трехзначное число?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.