Задачи ЕГЭ 2019

​

Задачи я записывал со слов, но не решал. Некоторые условия могут оказаться неправильными.

13 задача

1) Решите уравнение \(6\cos^2x+5\sqrt2\sin x+2=0\).

2) Решите уравнение \(\cos2x+\sqrt2\cos\left( \dfrac{\pi}2+ x\right)+1=0\).

3) Решите уравнение \(\cos2x+\sqrt3\cos\left( \dfrac{\pi}2- x\right)+2=0\).

4) Решите уравнение \(4\cos^2x+\sin\left( \dfrac{3\pi}2- x\right)-5=0\).

5) Решите уравнение \(2\cos^2x+2\sqrt2\sin\left( \dfrac{\pi}2- x\right)+1=0\).

6) Решите уравнение \(2\cos^2x+\sqrt3\sin2x+1=0\).

7) Решите уравнение \(8\sin^2x-2\sqrt3\cos\left( \dfrac{\pi}2- x\right)-9=0\).

8) Решите уравнение \(2\sin^2x-2\sqrt2\cos x+1=0\).

9) Решите уравнение \(2\sin^2x+3\sqrt3\sin\left( \dfrac{\pi}2+ x\right)+4=0\).

10) Решите уравнение \(2\cos^2x+\sqrt3\sin\left( \dfrac{3\pi}2+x\right)+1=0\).

11) Решите уравнение \(2\sin^2x+3\sqrt2\sin\left( \dfrac{3\pi}2- x\right)-4=0\).

12) Решите уравнение \(\cos2x+\sin^2 x=0{,}25\).

14 задача

1) В правильной треугольной пирамиде SABC сторона основания равна 6, а боковое ребро SA равно 7. Точки M и N принадлежат ребрам AB и SC соответственно, причем AM:BM=SN:CN=5:1. Плоскость \(\alpha\) содержит прямую MN и параллельна ребру SA.
а) Докажите, что плоскость \(\alpha\) параллельна ребру BC.
б) Найдите расстояни от точки C до плоскости \(\alpha\).

2) Дана правильная четырёхугольная пирамида SABCD с вершиной S. AB=3, SA=6. Точка K лежит на SC. SK:KC=1:2. Плоскость \(alpha\) проходит через точку K и параллельна плоскости SAD. 
a) Докажите, что сечение пирамиды SABCD плоскостью \(alpha\) является равнобедренной трапецией. 
б) Найдите объём пирамиды, основанием которой является это сечение и вершиной S.

3) В правильной треугольной пирамиде SABC сторона основания равна 3, а боковое ребро SA равно 4. Точки M и K принадлежат ребрам SC и AB соответственно, причем AK:KB=SM:MC=1:2. Плоскость \(\alpha\) содержит прямую MK и параллельна ребру BC.
а) Докажите, что плоскость \(\alpha\) параллельна ребру SA.
б) Найдите расстояни от точки A до плоскости \(\alpha\).

15 задача

1) Решите неравентсво \(\log_{\frac13}(18-9x)<\log_{\frac13}(x^2-6x+8)+\log_{\frac13}(x+2)\).

2) Решите неравентсво \(\log_{0{,}5}(10-10x)<\log_{0{,}5}(x^2-5x+4)+\log_{0{,}5}(x+3)\).

3) Решите неравентсво \(\log_{4}(24-12x)<\log_{4}(x^2-7x+10)+\log_{4}(x+3)\).

4) Решите неравентсво \(\log_{2}(14-14x)\geqslant \log_{2}(x^2-5x-14)+\log_{2}(x+5)\).

5) Решите неравентсво \(\log_{4}(16-16x)<\log_{4}(x^2-3x+2)+\log_{4}(x+6)\).

6) Решите неравентсво \(\log_{2}(14-14x)<\log_{2}(x^2+5x-4)+\log_{2}(x-5)\).

7) Решите неравентсво \(\log_{0{,}1}(6-6x)<\log_{0{,}1}(x^2-4x+3)+\log_{0{,}1}(x+4)\).

8) Решите неравентсво \(\log_{6}(108-36x)>\log_{6}(x^2-11x+24)+\log_{6}(x+4)\).

9) Решите неравентсво \(\log_{0{,}6}(18-18x)<\log_{0{,}6}(x^2-6x+5)+\log_{0{,}6}(x+4)\).

10) Решите неравентсво \(\log_{3}(9-9x)\geqslant \log_{3}(x^2-3x+2)+\log_{3}(x+4)\).

11) Решите неравентсво \(\log_{5}(25-25x)\geqslant \log_{5}(x^2-4x+3)+\log_{5}(x+7)\).

12) Решите неравентсво \(\log_4(6-6x)\geqslant \log_4(x^2-5x+4)-\log_4(x+3)\).

13) Решите неравентсво \(\log_{3}(4-4x)\geqslant \log_{3}(x^2-4x+3)+\log_{3}(x+2)\).

16 задача

1) Точка O – центр вписанной в треугольник ABC окружности. Луч BO пересекает описанную окружность в точке P.
а) Докажите, что угол POC равен углу PCO.
б) Найдите площадь треугольника APC, если радиу описанной около ABC окружности равен 4, а угол ABC равен 120°.

Решение

2) Треугольник ABC остроугольный, BH – высота. Продолжение BH пересекает описанную около этого треугольника окружность в точке K. BN – диаметр описанной около ABC окружности.
а) Докажите, что AN=CK.
б) Если знаете, что было в этом пункте, напишите в комментариях.

Решение

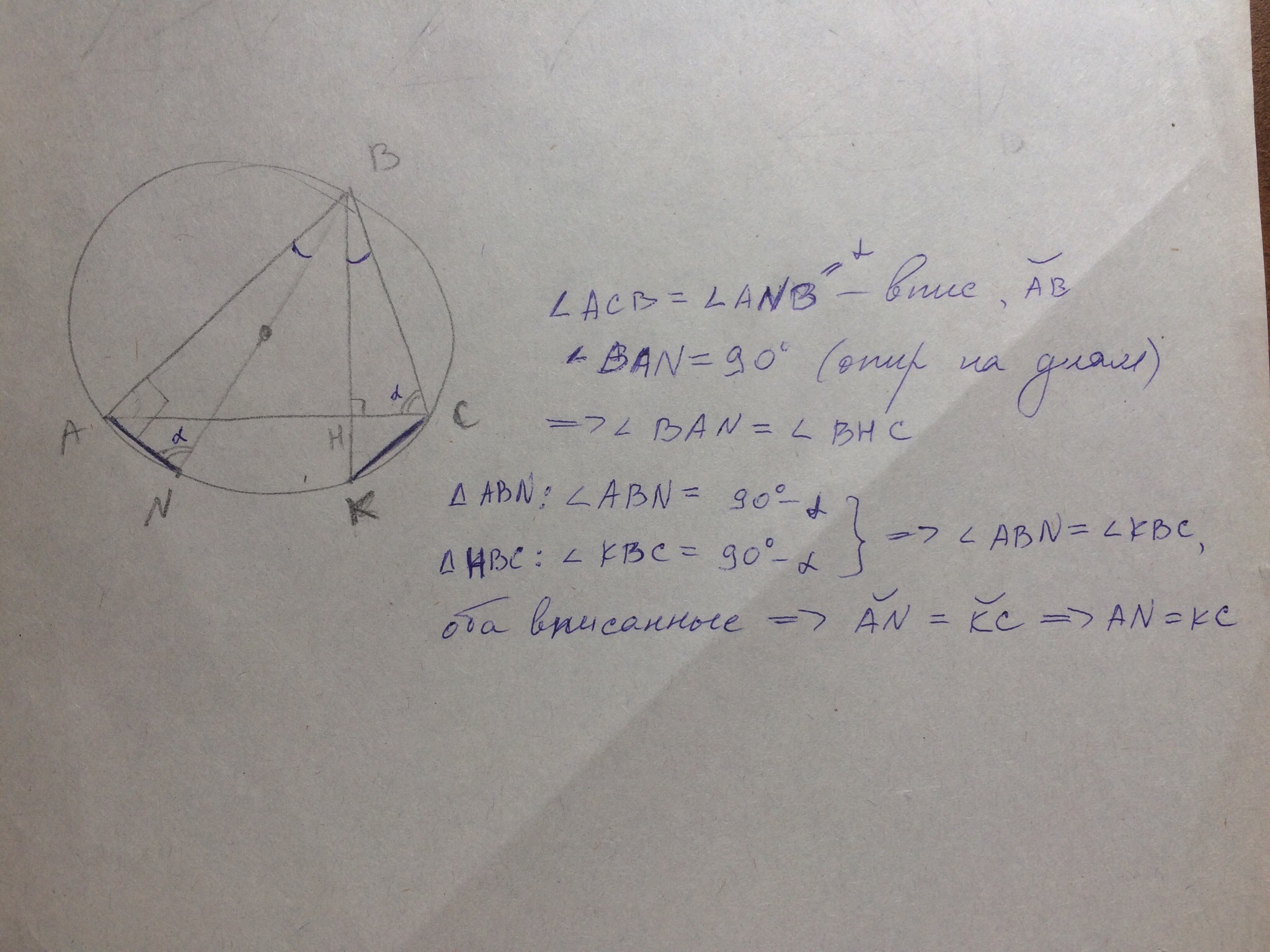
3) Точка O – центр вписанной в треугольник ABC окружности. Луч BO пересекает описанную окружность в точке P.
а) Докажите, что PO=PC.
б) ? (напишите в комментах, если знаете)

17 задача

1) В июле планируется взять кредит в банке на сумму 6 млн рублей на срок 15 лет. Условия его возврата таковы:
– каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года надо выплатить часть долга;
– в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платеж по кредиту составил не более 1,9 млн рублей, а наименьший – не менее 0,5 млн рублей.

2) 15 января планируется взять кредит в банке на сумму на срок 39 месяцев. Условия его возврата таковы:
– 1 января каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Найдите r, если известно, что общая сумма выплат на 20% больше суммы взятой в кредит.

18 задача

1) Найдите все значения параметра \(a\), при которых уравнение \(\dfrac{x^2-4x+a}{5x^2-6ax+a^2}=0\) имеет ровно два корня.

2) Найдите все значения параметра \(a\), при которых уравнение \(\dfrac{|3x|-2x-2-a}{x^2-2x-a}=0\) имеет ровно два корня.

3) Найдите все значения параметра \(a\), при которых уравнение \(\dfrac{x^2-2x+a}{4x^2-3ax-a^2}=0\) имеет ровно два корня.

4) Найдите все значения параметра \(a\), при которых уравнение \(\dfrac{x^2-2x+a^2-4}{x^2-a}=0\) имеет ровно два корня.

5) Найдите все значения параметра \(a\), при которых уравнение \(\dfrac{|4x-15|+2a-15}{x^2-10x+a^2}=0\) имеет ровно два корня.

6) Найдите все значения параметра \(a\), при которых уравнение \(\dfrac{x^2-2x+a^2-4a}{x^2-a}=0\) имеет ровно два корня.

7) Найдите все значения параметра \(a\), при которых уравнение \(\dfrac{|4x|-x-3-a}{x^2-x-a}=0\) имеет ровно два корня.

8) Найдите все значения параметра \(a\), при которых уравнение \(\dfrac{x^2-4x+a}{x^2-ax+a^2}=0\) имеет ровно два корня.

9) Найдите все значения параметра \(a\), при которых уравнение \(\dfrac{x^2-6x+a^2+2a}{2x^2-ax-a^2}=0\) имеет ровно два корня.

10) Найдите все значения параметра \(a\), при которых уравнение \(\dfrac{x^2-4x+a^2-2a}{x^2+ax-6a^2}=0\) имеет ровно два корня.

Решение графически

Решение аналитически

19 задача

1) Дана последовательность из 100 натуральных чисел, каждое из которых, начиная со второго, либо в два раза больше предыдущего, либо на 98 меньше.
а) Может ли последовательность состоять из 5 различных чисел?
б) Какое может быть \(a_1\), если \(a_{100}=75\).
в) Найдите наименьшее значение наибольшего члена последовательности.

2) В корзине лежит 95 фруктов. Средняя масса всех фруктов 100 г. Средняя масса тех, которые легче 100 г, 73 грамма. Средняя масса тех, которые тяжелее 100 г, 115 грамм.
а) Может ли быть поровну фруктов, масса которых меньше 100 г, и фруктов, масса которых больше 100 г?
б) Может ли быть меньше 10 фруктов, чья масса равна 100 г?
в) Найдите максимальную массу фрукта в корзине.

3) Есть 40 карточек красного и синего цвета. На них написаны натуральные числа. На красных все числа разные, а на синих любое число больше любого числа на красных. Среднее арифметическое всех чисел 14,5. Затем, все числа  на синих карточках умножили на 3 и среднее арифметическое всех чисел стало равным 41.
а) Могло ли быть 10 красных карточек?
б) Могло ли быть 4 красные карточки?
в) Какое наибольшее число могло быть написано на синей карточке?

4) На столе лежат 50 карточек. Часть из них синие, другая - красные. Все числа на синих карточках разные, любое число на синей карточке больше любого числа на красной. 
а) Могло ли быть ровно 10 синих карточек?
б) Могло ли быть ровно 10 красных карточек?
в) Какое наименьшее количество синих карточек могло быть?

• ← Назад
• Далее →