Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ профиль 10.19
В спортивном лагере по настольному теннису каждый день ломается или теряется 7 теннисных шариков. Лагерная смена длится 14 дней. Шарики продают в упаковках по 12 штук. Какое наименьшее количество упаковок шариков нужно купить на одну смену?
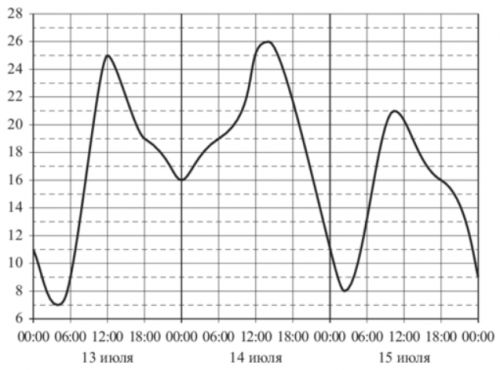
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 13 июля. Ответ дайте в градусах Цельсия.
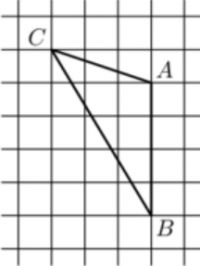
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его высоты, проведенной к прямой, содержащей сторону AB.
В группе туристов 300 человек. Их вертолётом доставляют в труднодоступный район, перевозя по 15 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист В. полетит первым рейсом вертолёта.
Найдите корень уравнения \(3^{3-x}=243\).
Площадь треугольника ABC равна 96, DE – средняя линия. Найдите площадь треугольника CDE.
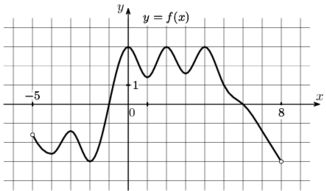
На рисунке изображен график функции \(y=f(x)\), определенной на интервале (-5;8). Найдите наименьшее значение функции \(f(x)\) на отрезке [-1;5].
Найдите объем шара, вписанного в конус объемом 36, если осевое сечение конуса является равносторонним треугольником.
Найдите значение выражения \(\sqrt{32}\cos^2\dfrac{7\pi}{8}-\sqrt{8}\).
Водолазный колокол, содержащий \(\nu=3\) моля воздуха при объём \(V_1=32\,л\) , медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма \(V_2\). Работа, совершаемая водой при сжатии воздуха, определяется выражением \(A=\alpha \nu T \log_2{\dfrac{V_1}{V_2}}\), где \(\alpha=11{,}5\, \dfrac{Дж}{моль\cdot К}\) – постоянная, \(T=200\, К\) – температура воздуха. Какой объём \(V_2\) в литрах станет занимать воздух в колоколе, если при сжатии воздуха была совершена работа в \(20700\, Дж\).
Заказ на 168 деталей первый рабочий выполняет на 2 часа быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый рабочий делает на 2 детали больше?
Найдите наименьшее значение функции \(y=5x-\ln(5x)+5\) на отрезке \(\left[\dfrac1{10};\dfrac12\right]\).
а) Решите уравнение \(4\cos^{2{,}5}x=\sqrt{\cos x}\)
б) Укажите все корни этого уравнения, принадлежащие отрезку \(\left[ \dfrac{5\pi}{2};\dfrac{7\pi}{2}\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
a)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 5π/2 | 18. 8π/3 | 19. 11π/4 | 20. 17π/6 |
| 21. 3π | 22. 19π/6 | 23. 13π/4 | 24. 10π/3 |
| 25. 7π/2 | 26. 11π/3 | 27. 15π/4 | 28. 23π/6 |
| 29. 4π |
Плоскость \(\alpha\) перпендикулярна основанию правильной треугольной пирамиды SABC и делит стороны AB и BC основания пополам.
а) Докажите, что плоскость \(\alpha\) делит боковое ребро в отношении 1:3, считая от вершины S.
б) Найдите отношение объемов многогранников (меньшего к большему), на которые плоскость \(\alpha\) разбивает пирамиду.
Запишите ответ в виде несократимого отношения, например "4:13".
Решите неравенство \(\log_{|x-2|}(3-|x|)\leqslant 1\).
Диагонали трапеции ABCD с основаниями AD и BC пересекаются в точке M. Окружность, описанная около треугольника CDM, пересекает отрезок AD в точке N и касается прямой BN.
а) Докажите, что треугольники BNC и CDN подобны.
б) Найдите AD, если CD=24, ∠BCD=∠DMA, а радиус окружности равен 13.
В июле 2019 года планируется взять кредит в банке на 6 лет в размере 880000 рублей. Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с долгом на конец предыдущего года;
– с февраля по июнь ежегодно необходимо выплатить по 250 000 рублей;
– в 2024 и 2025 годах дополнительно производятся выплаты по B рублей;
– к июлю 2025 года долг будет выплачен полностью.
Найдите B.
Найдите все значения параметра \(a\), при которых система
\(\begin{cases} x^2+(5a+2)x+4a^2+2a<0\\x^2+a^2=4\end{cases}\)
имеет хотя бы одно решение.
Задуман набор последовательных (идущих подряд) натуральных чисел, сумма которых больше 231 и меньше 245.
а) Может ли в наборе быть 13 чисел?
б) Может ли в наборе быть 14 чисел?
в) Какое наибольшее количество чисел, которые удовлетворяют заданному условию, может быть задумано?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.