Вариант ЕГЭ 15.18 (1-12)

Бегун пробежал 60 м за 6 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.

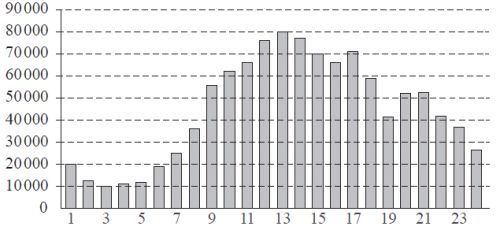
На диаграмме показано количество посетителей сайта в течение каждого часа 5 марта 2011 года. По горизонтали указывается номер часа, по вертикали - количество посетителей сайта за данный час. Определите по диаграмме разность наибольшего и наименьшего количества посетителей за час в данный день

На клечатой бумаге изображены два круга. Найдите площадь большего круга, если площадь закрашенной фигуры равна 64.

В соревнованиях участвуют 12 спортсменов. С помощью жребия их нужно распределить на четыре группы по три человека в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4. Спортсмены тянут по одной карточке. Какова вероятность того, что спортсмен из Киргизии окажется в третьей группе?

Найдите корень уравнения: \(18^{8-x}=324^{2x}\).

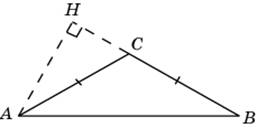
В треугольнике \(ABC\) \(AC=BC=8\sqrt{3}\), угол \(C\) равен \(120^{\circ}\). Найдите высоту \(AH\).

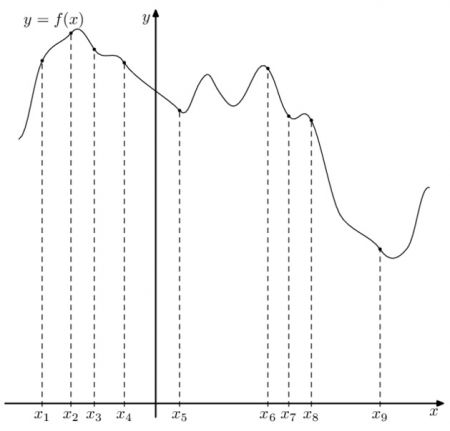
На рисунке изображён график функции \(y=f(x)\) и девять точек на оси абсцисс: \( x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9\). В скольких из этих точек производная функции \(f(x)\) отрицательна?

Во сколько раз уменьшится объём конуса, если его высота уменьшится в 3 раза, а радиус основания останется прежним?

Найдите значение выражения \(\dfrac{-10\sin371^{\circ}}{\sin11^{\circ}}\).

Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой \(m=13\,кг\) и радиуса \(R=4\,см\), и двух боковых с массами \(M=9\,кг\) и радиусами \(R+h\). При этом момент инерции катушки относительно оси вращения, выражаемый в \(кг \cdot см^{2}\), задаётся формулой \(I=\dfrac{(m+2M)R^{2}}{2}+M(2Rh+h^{2})\). При каком максимальном значении \(h\) момент инерции катушки не превышает предельного значения \(545\) \(кг \cdot см^{2}\)? Ответ выразите в сантиметрах.

В сосуд, содержащий 12-процентный раствор некоторого вещества добавили вдвое меньшее количество раствора этого же вещества. Концентрация получившегося раствора составила 18%. Сколько процентов составляла концентрация добавленного раствора?

Найдите точку максимума функции \(y=\dfrac{x^{3}}{3}-16x+1\).