Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ 16.18 (1-12;15)
Разбор варианта
\(\boxed{1}\) В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 20% от стоимости купленной мебели. Прикроватная тумбочка стоит 2500 рублей. Во сколько рублей обойдётся покупка этой тумбочки вместе со сборкой?
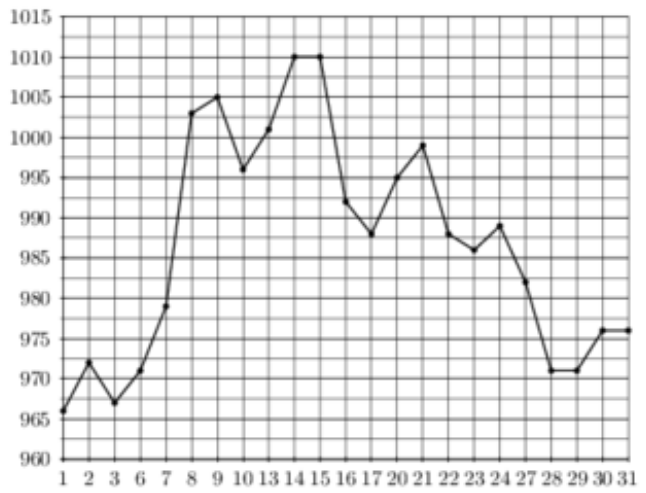
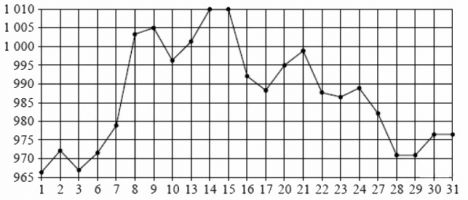
\( \boxed{2}\) На рисунке жирными точками показана цена некоторого товара, установленная Центробанком РФ во все рабочие дни в октябре 2009 года. По горизонтали указываются числа месяца, по вертикали – цена товара в рублях за единицу. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена товара была наименьшей за указанный период.
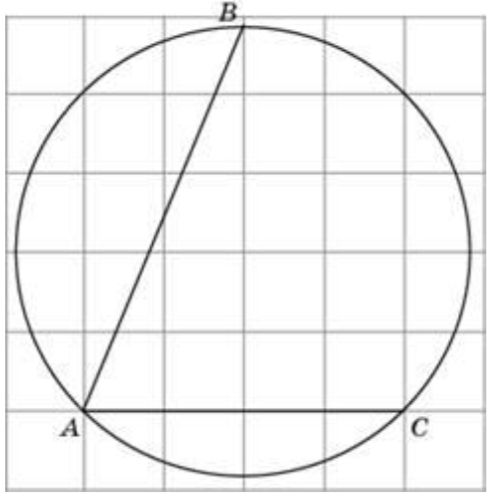
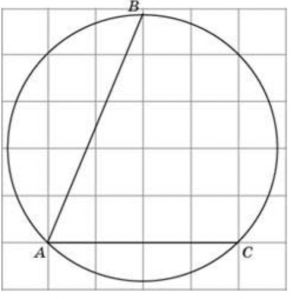
\( \boxed{3} \) Найдите градусную меру дуги \(BC\) окружности, на которую опирается угол \( BAC\). Ответ дайте в градусах.
\( \boxed{4} \) Магазин покупает куриные яйца у двух ферм. 85% яиц от первой фермы – яйца высшей категории, а от второй – 10% яиц высшей категории. Всего высшую категорию получает 55% яиц. Найдите вероятность того, что яйцо, купленное в этом магазине окажется от первой фермы.
\( \boxed{5} \) Решите уравнение \( \log_7(3-2x)=\log_7{11} \).
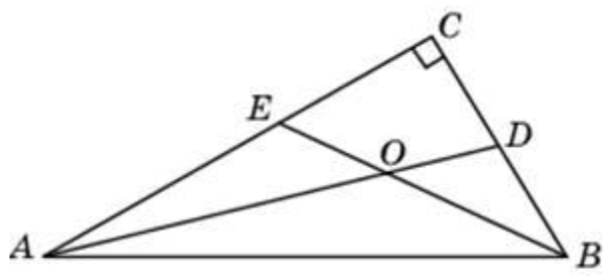
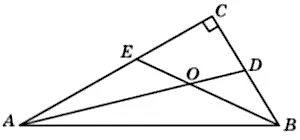
\( \boxed{6} \) Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
\( \boxed{7} \) Прямая \(y=3x+1 \) является касательной к графику функции \( f(x)=ax^2+2x+3 \). Найдите \(a\).
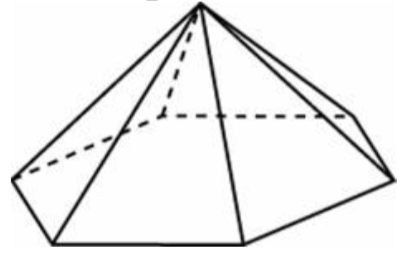
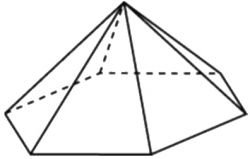
\( \boxed{8} \) Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
\( \boxed{9} \) Найдите значение выражения \( \dfrac{(12\sqrt2)^2}{3} \).
\( \boxed{10} \) На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция
имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: \( F_A=\rho g l^3\) , где \( l\) – длина ребра куба в метрах, \( \rho=1000\, кг/м^3\) – плотность воды, а \( g\) – ускорение свободного падения (считайте \( g =9{,}8\) Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 321126,4 Н? Ответ выразите в метрах.
\( \boxed{11} \) В сосуд, содержащий 8 литров 24-процентного водного раствора некоторого вещества, добавили 4 литра воды. Сколько процентов составляет концентрация получившегося раствора?
\( \boxed{12} \) Найдие наименьшее значение функции \( y=x^3+12x^2+36x+52\) на отрезке \([-4{,}5;1]\).
\( \boxed{15} \) Решите неравенство \( \dfrac{\log_2(3\cdot 2^{x-1} - 1)}{x}\geqslant 1 \).
В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 20% от стоимости купленной мебели. Прикроватная тумбочка стоит 2500 рублей. Во сколько рублей обойдётся покупка этой тумбочки вместе со сборкой?
На рисунке жирными точками показана цена некоторого товара, установленная Центробанком РФ во все рабочие дни в октябре 2009 года. По горизонтали указываются числа месяца, по вертикали – цена товара в рублях за единицу. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена товара была наименьшей за указанный период.
Найдите градусную меру дуги \(BC\) окружности, на которую опирается угол \(BAC\). Ответ дайте в градусах.
Магазин покупает куриные яйца у двух ферм. 85% яиц от первой фермы – яйца высшей категории, а от второй - 10% яиц высшей категории. Всего высшую категорию получает 55% яиц. Найдите вероятность того, что яйцо, купленное в этом магазине окажется от первой фермы.
Решите уравнение \(\log_7(3-2x)=\log_7{11}\).
Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Прямая \(y=3x+1\) является касательной к графику функции \(f(x)=ax^2+2x+3\). Найдите \(a\).
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Найдите значение выражения \(\dfrac{(12\sqrt2)^2}{3}\).
На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: \( F_A=\rho g l^3\) , где \( l\) – длина ребра куба в метрах, \( \rho=1000\, кг/м^3\) – плотность воды, а \( g\) – ускорение свободного падения (считайте \( g =9{,}8\) Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 321126,4 Н? Ответ выразите в метрах.
В сосуд, содержащий 8 литров 24-процентного водного раствора некоторого вещества, добавили 4 литра воды. Сколько процентов составляет концентрация получившегося раствора?
Найдите наименьшее значение функции \(y=x^3+12x^2+36x+52\) на отрезке \([-4{,}5;1]\).
Решите неравенство \(\dfrac{\log_2(3\cdot 2^{x-1} - 1)}{x}\geqslant 1\).