Вариант ЕГЭ 1.18 (1-12)

Сырок стоит 8 рублей 20 копеек. Какое наибольшее число сырков можно купить на 50 рублей?

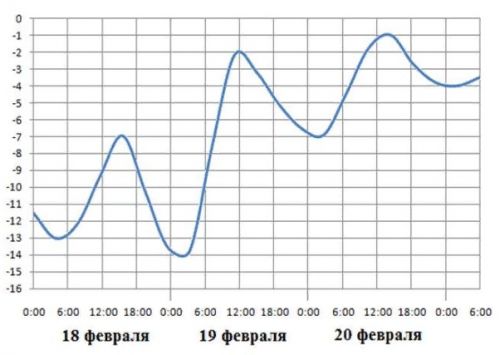
На рисунке показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали – значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру 20 февраля. Ответ дайте в градусах Цельсия.

​

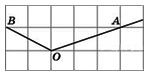
На клетчатой бумаге с размером клетки 1×1 изображен угол. Найдите тангенс этого угла.

​

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 10. Результат округлите до сотых.

Найдите корень уравнения \(3^{8-x}=27\)

В треугольнике \(ABC\) \(AC = BC = 20\), \(AH\) – высота, \(\sin BAC = 0{,}25\). Найдите \(BH\).

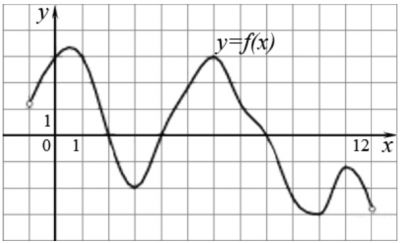
На рисунке изображен график функции \(y = f(x)\), определенной на интервале (-1;12). Определите количество целых точек, в которых производная функции будет отрицательна.

В цилиндрический сосуд налили 2000 см³ воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объём детали? Ответ выразите в см³.

Найдите значение выражения \(\sqrt{65^2-56^2}\)

При температуре \(0°C\) рельс имеет длину \(l_0 = 10\)м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону \(l(t°) = l_0(1 + a ⋅ t°)\), где \(a = 1{,}2\cdot 10^{-5}(°C)^{-1}\) – коэффициент теплового расширения, \(t°\) – температура (в градусах Цельсия). При какой температуре рельс удлинится на 7,5 мм? Ответ выразите в градусах Цельсия.

Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 42 км/ч, а вторую половину пути – со скоростью, на 8 км/ч большей скорости первого, в результате чего прибыл в город B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.

Найдите наименьшее значение функции \(y = (x-24)e^{x-23}\) на отрезке \([21;24]\).