Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ профиль 4.20
Тетрадь стоит 30 рублей. Какое наибольшее количество таких тетрадей можно будет купить на 150 рублей после понижения цены на 30%?
На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси — крутящий момент в Н⋅м. Определите по графику, на сколько увеличился крутящий момент, если двигатель увеличил число оборотов с 1000 до 2000. Ответ дайте в Н⋅м.
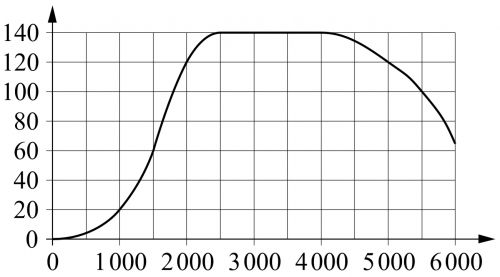
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 3 прыгуна из Голландии и 6 прыгунов из Аргентины. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что тринадцатым будет выступать прыгун из Аргентины.
Найдите корень уравнения \(5^{x-6}=25^{2x}\).
Два угла вписанного в окружность четырёхугольника равны 62° и 98°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
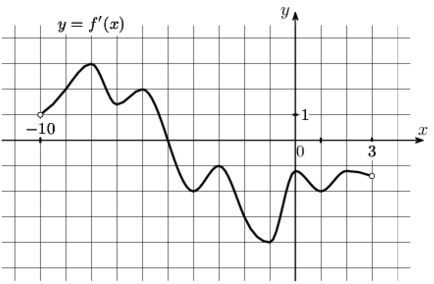
На рисунке изображен график \(y=f'(x)\) — производной функции \(f(x)\), определенной на интервале \((-10;3)\). В какой точке отрезка \([-5;1]\) функция \(f(x)\) принимает наименьшее значение?
Площадь основания конуса равна 48. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 15 и 45, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Найдите значение выражения \(5\sqrt2\sin\dfrac{3\pi}8\cdot \cos\dfrac{3\pi}8\)
Два тела массой \(m=4кг\) каждое движутся с одинаковой скоростью \(v =9 м/с\) под углом \(2α\) друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле \(Q=mv^2\sin^2α\), где \(m\) — масса (в кг), \(v\) — скорость (в м/с). Найдите, под каким углом \(2α\) должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 243 Дж. Ответ дайте в градусах.
Имеется два сплава. Первый содержит 15% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 140 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Найдите наибольшее значение функции \(y=(x-3)^2(x+6)+9\) на отрезке [-10;0].
а) Решите уравнение \(2\sin(\pi+x)\cdot \sin\left( \dfrac{\pi}{2}+x\right)=\sin x\)
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[ 3\pi; \dfrac{9\pi}{2}\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17.3π | 18.19π/6 | 19. 13π/4 | 20. 10π/3 |
| 21.7π/2 | 22.11π/3 | 23. 15π/4 | 24.23π/6 |
| 25. 4π | 26. 25π/6 | 27. 17π/4 | 28.13π/3 |
| 29.9π/2 |
В основании правильной пирамиды PABCD лежит квадрат ABCD со стороной 6. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды.
Решите неравенство \(\log_{(x+4)^2}(3x^2-x-1)\leqslant 0\).
Окружность с центром в точке O проходит через вершины C и D большей боковой стороны прямоугольной трапеции ABCD, пересекает второй раз основания AD и BC в точках L и P соответственнои касется боковой стороны AB в точке T.
а) Докажите, что угол COD в два раза больше угла CTD.
б) Найдите расстояние от точки T до прямой CD, если основания трапеции AD и BC равны соответственно 9 и 4.
В июле планируется взять кредит на сумму 69 510 рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 10 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить некоторую часть долга.
На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен тремя равными платежами (то есть за три года), по сравнению со случаем, если кредит будет полностью погашен двумя равными платежами (то есть за два года)?
Найдите все значения параметра \(a\), при каждом из которых система уравнений \(\begin{cases}2x^2+2y^2=5xy\\(x-a)^2+(y-a)^2=5a^4\end{cases}\) имеет ровно два решения.
Последовательность \(a_1, a_2, ..., a_n, ...\) состоит из натуральных чисел, причём \(a_{n+2}=a_{n+1}+a_n\) при всех натуральных \(n\).
а) Может ли выполняться равенство \(4a_5=7a_4\)?
б)Может ли выполняться равенство \(5a_5=7a_4\)?
в) При каком наибольшем натуральном \(n\) может выполняться равенство \(6n\cdot a_{n+1}=(n^2+24)a_n\)?
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.