Вариант ЕГЭ профиль 7.19

На автозаправке один литр бензина стоит 35 руб. 60 коп. Водитель залил в бак 30 литров и взял бутылку воды за 35 рублей. Сколько рублей сдачи он получит с 1500 рублей?

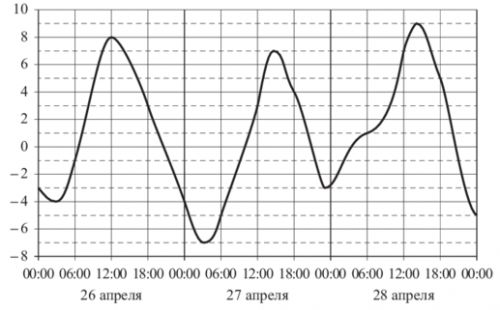
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 27 апреля. Ответ дайте в градусах Цельсия.

На клетчатой бумаге с размером клетки \(1\times 1\) изображен параллелограмм. Найдите длину его меньшей диагонали.

При изготовлении подшипников диаметром 76 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,983. Найдите вероятность того, что случайный подшипник будет иметь иметь диаметр меньше чем 75,99 мм или больше чем 76,01 мм.

Найдите корень уравнения \(\dfrac{1}{12x-11}=\dfrac14\).

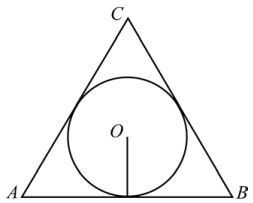
Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника.

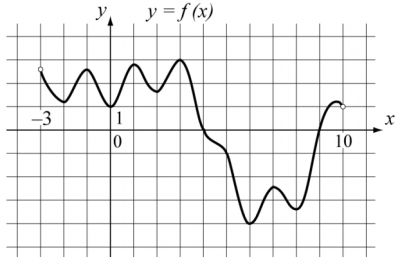
На рисунке изображен график функции \(y=f(x)\), определенной на интервале (-3;10). Найдите количество точек, в которых производная функции \(f(x)\) равна 0.

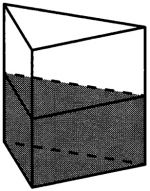
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в 2 раза больше, чем у первого? Ответ выразите в сантиметрах.

Найдите значение выражения \((\sqrt{48}-\sqrt{3})\cdot \sqrt{12}\).

При нормальном падении света с длиной волны \(\lambda=650\, нм\) на дифракционную решетку с периодом \(d\) нм наблюдают серию дифракционных максимумов. При этом угол \(\alpha\) (отсчитываемый от перпендикуляра к решетке), под которым наблюдается максимум, и номер максимума \(k\) связаны соотношением \(d\cdot \sin\alpha=k\lambda\). Под каким минимальным углом \(\alpha\) (в градусах) можно наблюдать третий максимум на решетке с периодом, не превосходящим 1950 нм?

От пристани А к пристани В, расстояние между которыми равно 182 км, отправился с постоянной скоростью первый теплоход, а через час после этого следом за ним со скоростью, на 1 км/ч большей, отправился второй. Найдите скорость второго теплохода, если в пункт В он прибыл одновременно с первым. Ответ дайте в км/ч.

Найдите наименьшее значение функции \(y=(x+26)^2\cdot e^{-26-x}\) на отрезке [-27;-25].

а) Решите уравнение \(8\sin^2\left( \dfrac{7\pi}{12}+x \right)-2\sqrt3\cos 2x=5\).
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[ -\dfrac{7\pi}{2};-\dfrac{5\pi}{2}\right]\).

Выберите все верные ответы на пункты а) и б).

В основании правильной четырехугольной пирамиды MABCD лежит квадрат ABCD со стороной 6. Противоположные боковые ребра пирамиды попарно перпендикулярны. Через середины ребер MA и MB проведена плоскость \(\alpha\), параллельная ребру MC.
а) Докажите, что сечение плоскостью \(\alpha\) пирамиды MABC является параллелограммом.
б) Найдите площадь сечения пирамиды MABC плоскостью \(\alpha\).

Решите неравенство \(x^3+2x^2-\dfrac{24x^2-x+3}{x-3}\leqslant 1\).

Две окружности касаются внешним образом в точке C. Прямая касается меньшей окружности в точке A, а большей — в точке B, отличной от A. Прямая AC второй раз пересекает большую окружность в точке D, прямая BC второй раз пересекает меньшую окружность в точке E.
а) Докажите, что прямая AE параллельна прямой BD.
б) Пусть L — отличная от D точка пересечения отрезка DE с большей окружностью. Найдите EL, если радиусы окружностей равны 2 и 5.

Бернард планирует вложить в четырехлетний проект целое число млн рублей. По итогам каждого года планируется прирост средств вкладчика на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 15млн рублей в первый и второй годы, а также по 10млн в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений (в млн) , при котором общая сумма средств вкладчика к началу третьего года станет больше 110 млн, а к концу проекта — больше 190 млн рублей.

Найдите все значения параметра \(a\). при которых уравнение \((x^2+2x+2a)^2=5x^4+5(x+a)^2\) имеет ровно одно решение на отрезке [0;2].

Пусть K(n) обозначает сумму квадратов всех цифр натурального числа n.
а) Существует ли такое трёхзначное число n, что K(n)=171?
б)Существует ли такое трёхзначное число n, что K(n)=172?
в) Какое наименьшее значение может принимать выражение 4K(n)-n, если n — трёхзначное число?

Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы