Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ профиль 2.19
В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 270 листов. Какого наименьшего количества пачек бумаги хватит на 6 недель?
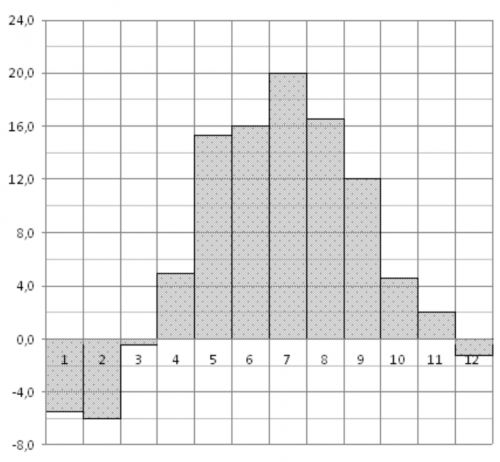
На диаграмме показана среднемесячная температура в городе N за каждый месяц 2001 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру за первое полугодие этого года.
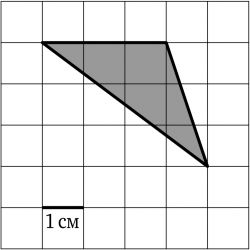
На клетчатой бумаге с размером клетки \(1 см \times 1 см\) изображен треугольник. Найдите его площадь, ответ дайте в квадратных сантиметрах.
Вероятность того, что новый фен прослужит больше года, равна 0,9. Вероятность того, что он прослужит два года или больше, равна 0,82. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Решите уравнение \( \dfrac89x=18{\dfrac23}\).
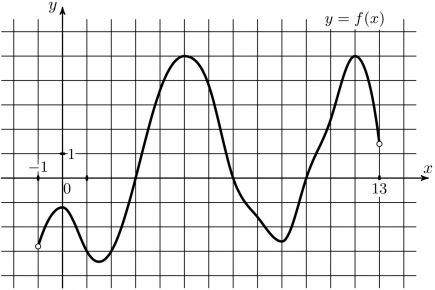
На рисунке изображен график функции \(y=f(x)\), определенной на интервале (-1;13). Найдите количество целых точек, в которых производная функции \(f(x)\) положительна.
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна \(\sqrt3\).

Найдите значение выражения \( \sqrt{11}(\sqrt{11}-\sqrt{99})\).
Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой \(\nu=\dfrac{T_1-T_2}{T_1}\cdot 100\%\), где \(T_1\)– температура нагревателя (в градусах Кельвина), \(T_2\) – температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя \(T_1\) КПД этого двигателя будет не меньше 50%, если температура холодильника \(T_2=250 \,К\)? Ответ дайте в кельвинах.
Два велосипедиста одновременно отправились в 224-километровый пробег. Первый ехал со скоростью, на 2 км/ч большей, чем скорость второго, и прибыл к финишу на 2 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Найдите наименьшее значение функции \(y=x^3-147x+19\) на отрезке [0;8].
а) Решите уравнение \(\sin2x=\cos(x-\frac{3\pi}2)\)
б) Найдите все его корни, принадлежащие отрезку \(\left[ 2\pi;\frac{7\pi}{2}\right]\)
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 2π | 18. 13π/6 | 19. 9π/4 | 20. 7π/3 |
| 21. 5π/2 | 22. 8π/3 | 23. 11π/4 | 24. 17π/6 |
| 25. 3π | 26. 19π/6 | 27. 13π/4 | 28. 10π/3 |
| 29. 7π/2 |
На ребре SA правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM:МА=5:1. Точки P и Q — середины рёбер ВС и AD соответственно.
а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией.
б) Найдите отношение объёмов многогранников (меньшего к большему), на которые плоскость MPQ разбивает пирамиду.
Запишите ответ в виде несократимого отношения, например "4:13".
Найдите наибольший отрицательный корень уравнения \(4\sin\left(\dfrac{3\pi}2+\dfrac{\pi x}{12}\right)=-\sqrt{12}\)
В прямоугольном треугольнике \(ABC\) угол при вершине \(A\) равен 30°. Точка \(D\) – середина гипотенузы \(AB\). Окружности, вписанные в треугольники \(ADC\) и \(BDC\) касаются сторон \(AC\) и \(BC\) в точках \(K\) и \(P\) соответственно.
а) Докажите, что \(KP\) равно \(CD\).
б) Найдите, в каком отношении делит гипотенузу \(AB\) точка касания большей из этих окружностей, считая от вершины \(A\).
Ответ запишите в виде несрократимого отношения без пробелов, например "4:13".
В июле планируется взять кредит в банке на некоторую сумму рублей. Условия его возврата таковы:
– каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга, равную 216 тысяч рублей.
Сколько тысяч рублей было взято в банке, если известно, что кредит был полностью погашен тремя равными платежами (то есть за три года)?
Найдите все значения параметра \(a\), при которых уравнение \((x^2+x+a)^2=2x^4+2(x+a)^2\) имеет ровно одно решение на отрезке [0;2].
а) Существуют ли такие двузначные натуральные числа \(m\) и \(n\), что \(\left| \dfrac{m}{n}-\sqrt2\right| \leqslant \dfrac1{100}\)?
б) Существуют ли такие двузначные натуральные числа \(m\) и \(n\), что \(\left| \dfrac{m^2}{n^2}-2 \right| \leqslant \dfrac1{10000}\)?
в) Найдите все возможные значения натурального числа \(n\), при каждом из которых значение выражения \( \left| \sqrt2 - \dfrac{n+10}{n}\right|\) является наименьшим.
Введите ответ в форме строки "да;да;1234". Где ответы на пункты разделены ";", и первые два ответа с маленькой буквы.