Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ 18.18 (1-12)
Разбор варианта
\( \boxed{1}\) На автозаправке водитель попросил залить бензин до полного бака и отдал кассиру 2000 рублей. Цена бензина 45 руб. 20 коп. за литр. Клиент получил 146 руб. 80 коп. сдачи. Сколько литров бензина было залито в бак?
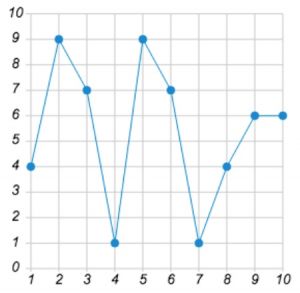
\( \boxed{2}\) На рисунке жирными точками показан путь, пройденный туристом за каждый день его путешествия. По горизонтали указываются дни его путешествия, по вертикали – количество километров, пройденных им в этот день.
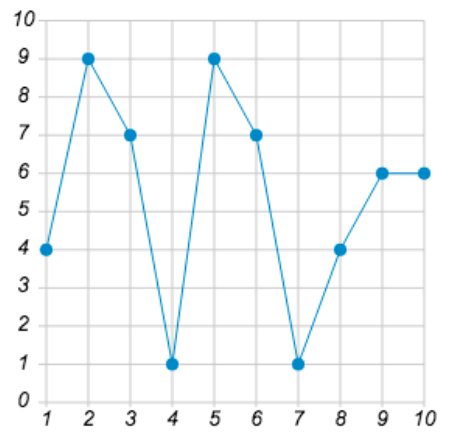
Определите по графику, сколько было дней, когда турист прошел больше, чем в восьмой день путешествия.
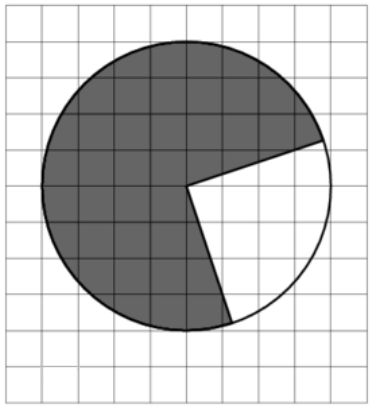
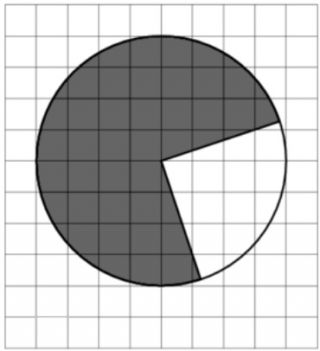
\( \boxed{3}\) На клетчатой бумаге с размером клетки \( \dfrac{2}{\sqrt{\pi}} \times \dfrac{2}{\sqrt{\pi}} \) изображён круг. Найдите площадь закрашенного сектора.
\( \boxed{4}\) В магазине четыре консультанта. Каждый из них занят с покупателем с вероятностью 0,8. Найдите вероятность того, что в случайный момент времени все четыре консультанта свободны одновременно (покупатели заходят независимо друг от друга).
\( \boxed{5}\) Найдите корень уравнения \( \sqrt{\dfrac{3}{5x-1}}=2 \).
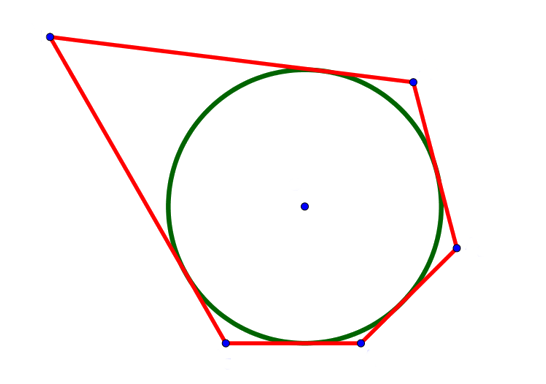
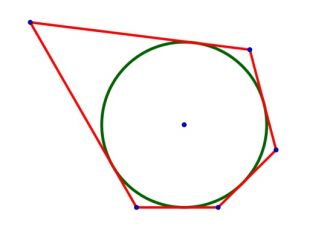
\( \boxed{6}\) Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 42. Найдите его площадь.
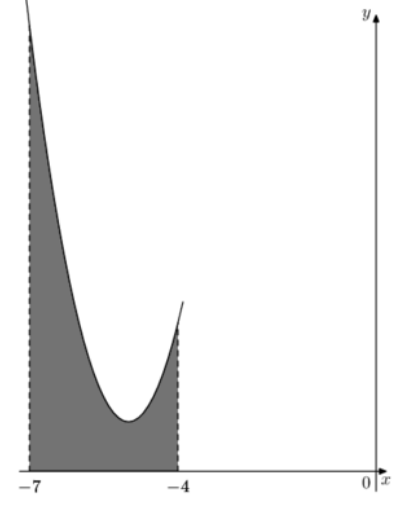
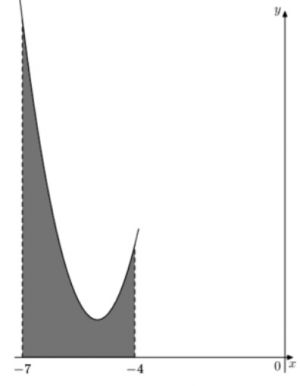
\( \boxed{7}\) На рисунке изображен график некоторой функции \( y=f(x) \), одна из первообразных которой \( F(x)=\dfrac23 x^3 +10x^2+51x-\dfrac{13}{21} \). Найдите площадь закрашенной фигуры.
\( \boxed{8}\) Найдите объем многогранника, вершинами которого являются точки \( A, B, B_1, C_1 \) прямоугольного параллелепипеда \( ABCDA_1B_1C_1D_1 \), у которого \(AB=5\), \(BC=3\), \(CC_1=4\).
\( \boxed{9}\) Вычислите \(27\cos 2\alpha\), если \(\sin \alpha=0{,}2\).
\( \boxed{10}\) Стоящий у платформы тепловоз издал гудок с частотой \( f_0=593 \)Гц. Затем гудок издал подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка \(f\) больше первого: она зависит от скорости тепловоза по закону \( f(v)=\dfrac{f_0}{1-\dfrac{v}{c}}\) Гц, где \(c\) – скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 7 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а \( c=300\) м/с. Ответ выразите в м/с.
\( \boxed{11}\) Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 21 килограммов изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
\( \boxed{12}\) Найдите наибольшее значение функции \( y=\dfrac{x^2+121}{x}\) на отрезке \( [1;20]\).
Ответы
1) 41
2) 6
3) 48
4) 0,0016
5) 0,35
6) 63
7) 9
8) 10
9) 21,84
10) 3,5
11) 199,5
12) 122
На автозаправке водитель попросил залить бензин до полного бака и отдал кассиру 2000 рублей. Цена бензина 45 руб. 20 коп. за литр. Клиент получил 146 руб. 80 коп. сдачи. Сколько литров бензина было залито в бак?
На рисунке жирными точками показан путь, пройденный туристом за каждый день его путешествия. По горизонтали указываются дни его путешествия, по вертикали – количество километров, пройденных им в этот день. Определите по графику, сколько было дней, когда турист прошел больше, чем в восьмой день путешествия.
На клетчатой бумаге с размером клетки \( \dfrac{2}{\sqrt{\pi}} \times \dfrac{2}{\sqrt{\pi}} \) изображён круг. Найдите площадь закрашенного сектора.
В магазине четыре консультанта. Каждый из них занят с покупателем с вероятностью 0,8. Найдите вероятность того, что в случайный момент времени все четыре консультанта свободны одновременно (покупатели заходят независимо друг от друга).
Найдите корень уравнения \( \sqrt{\dfrac{3}{5x-1}}=2\)
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 42. Найдите его площадь.
На рисунке изображен график некоторой функции \( y=f(x) \), одна из первообразных которой \( F(x)=\dfrac23 x^3 +10x^2+51x-\dfrac{13}{21} \). Найдите площадь закрашенной фигуры.
Найдите объем многогранника, вершинами которого являются точки A, B, B₁, C₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁, у которого AB=5, BC=3, CC₁=4.
Вычислите \(27\cos 2\alpha\), если \(\sin \alpha=0{,}2\).
Стоящий у платформы тепловоз издал гудок с частотой \(f_0=593\) Гц. Затем гудок издал подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка \(f\) больше первого: она зависит от скорости тепловоза по закону \( f(v)=\dfrac{f_0}{1-\dfrac{v}{c}}\) Гц, где \(c\) – скорость звука (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 7 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а \( c=300\) м/с. Ответ выразите в м/с.
Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 21 килограмма изюма, если виноград содержит 90% воды, а изюм содержит 5% воды?
Найдите наибольшее значение функции \( y=\dfrac{x^2+121}{x}\) на отрезке \( [1;20]\).