Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ 19.18 (1-12; 15)
Разбор варианта
\( \boxed{1}\) Блокнот стоит 30 рублей. Какое наибольшее количество таких блокнотов можно будет купить на 150 рублей после понижения цены на 30 %?
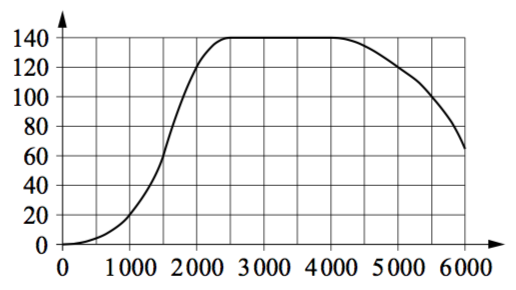
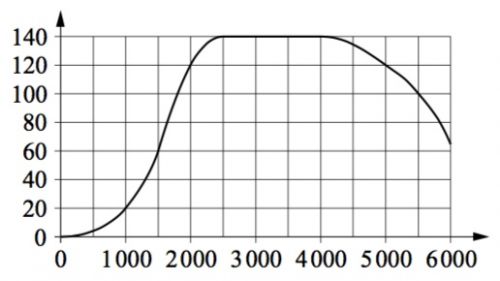
\( \boxed{2}\) На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси — крутящий момент в Н⋅м. Определите по графику, на сколько увеличился крутящий момент, если двигатель увеличил число оборотов с 1000 до 2000. Ответ дайте в Н⋅м.
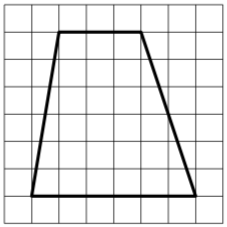
\( \boxed{3}\) На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.
\( \boxed{4}\) На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 8 прыгунов из Австрии и 6 прыгунов из Чехии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что тринадцатым будет выступать прыгун из Чехии.
\( \boxed{5}\) Найдите корень уравнения \(6^{x-6}=36^{2x}\).
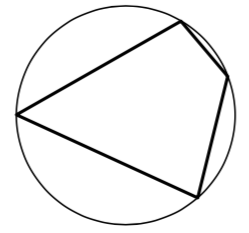
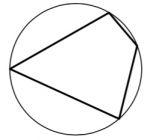
\( \boxed{6}\) Два угла вписанного в окружность четырёхугольника равны 52° и 96°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
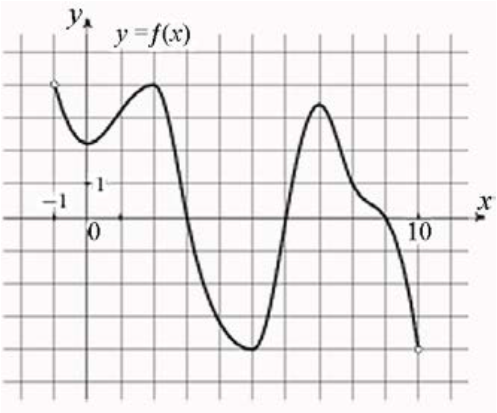
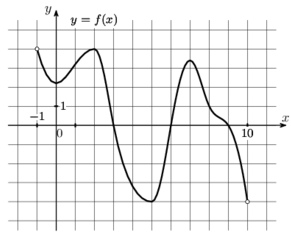
\( \boxed{7}\) На рисунке изображён график функции \( y = f (x) \), определённой на интервале \( (−1;10) \). Найдите количество точек, в которых производнаяфункции \(f(x)\) равна 0.
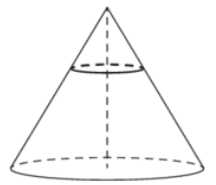
\( \boxed{8}\) Площадь основания конуса равна 63. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 1 и 2, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
\( \boxed{9}\) Найдите значение выражения \( \sin{\dfrac{5\pi}{12}}\cos{\dfrac{5\pi}{12}} \).
\( \boxed{10}\) Два тела массой \(m = 7\, кг\) каждое движутся с одинаковой скоростью \(v = 9\,м/c\) под углом \(2α\) друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле \(Q = mv^2 sin^2 α\) , где \(m\) — масса (в кг), \(v\) — скорость (в м/с). Найдите, под каким углом \(2α\) должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 567 Дж. Ответ дайте в градусах.
\( \boxed{11}\) Имеется два сплава. Первый содержит 10% никеля, второй — 25% никеля. Из этих двух сплавов получили третий сплав массой 105 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
\( \boxed{12}\) Найдите наибольшее значение функции \( y=(x−4)^2(x+8)−5\) на отрезке \([−20; 0]\).
\( \boxed{15}\) Решите неравенство \( \log_{(x+4)^2}(3x^2-x-1)\leqslant 0 \).
Ответы
1) 7
2) 100
3) 4,5
4) 0,15
5) -2
6) 128
7) 4
8) 7
9) 0,25
10) 180
11) 35
12) 251
15) \( (-5;-4)\cup (-4;-3)\cup \left[ -\dfrac23;\dfrac{1-\sqrt{13}}{6}\right) \cup \left(\dfrac{1+\sqrt{13}}{6};1\right] \)
Блокнот стоит 30 рублей. Какое наибольшее количество таких блокнотов можно будет купить на 150 рублей после понижения цены на \(30\%\)?
На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На горизонтальной оси отмечено число оборотов в минуту, на вертикальной оси — крутящий момент в Н⋅м. Определите по графику, на сколько увеличился крутящий момент, если двигатель увеличил число оборотов с 1000 до 2000. Ответ дайте в Н⋅м.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.

На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 8 прыгунов из Австрии и 6 прыгунов из Чехии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что тринадцатым будет выступать прыгун из Чехии.
Найдите корень уравнения \(6^{x-6}=36^{2x}\)
Два угла вписанного в окружность четырёхугольника равны 52° и 96°. Найдите больший из оставшихся углов. Ответ дайте в градусах.
На рисунке изображён график функции \( y = f (x) \), определённой на интервале \( (−1;10) \). Найдите количество точек, в которых производная функции \(f(x)\) равна 0.
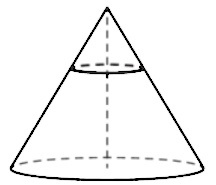
Площадь основания конуса равна 63. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 1 и 2, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Найдите значение выражения \( \sin{\dfrac{5\pi}{12}}\cos{\dfrac{5\pi}{12}} \).
Два тела массой \(m = 7\, кг\) каждое движутся с одинаковой скоростью \(v = 9\,м/c\) под углом \(2α\) друг к другу. Энергия (в Дж), выделяющаяся при их абсолютно неупругом соударении, вычисляется по формуле \(Q = mv^2 \sin^2 α\) , где \(m\) — масса (в кг), \(v\) — скорость (в м/с). Найдите, под каким углом \(2α\) должны двигаться тела, чтобы в результате соударения выделилась энергия, равная 567 Дж. Ответ дайте в градусах.
Имеется два сплава. Первый содержит 10% никеля, второй — 25% никеля. Из этих двух сплавов получили третий сплав массой 105 кг, содержащий 20% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Найдите наибольшее значение функции \( y=(x−4)^2(x+8)−5\) на отрезке \([−20; 0]\).
Решите уравнение \(\sqrt{3-2x}=x\). Если уравнение имеет более одного корня, в ответе запишите меньший из корней.