Варианты ЕГЭ профиль (с разбором)
Содержание
Вариант ЕГЭ 23.18 (1-12)
\(\boxed{1}\) Магазин закупает подсвечники по оптовой цене 150 рублей за штуку и продает с наценкой 30%. Какое наибольшее количество таких подсвечников можно купить в этом магазине на 1800 рублей?
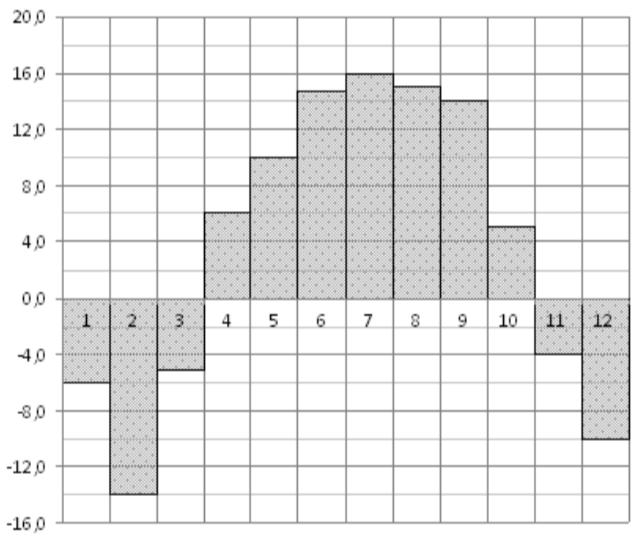
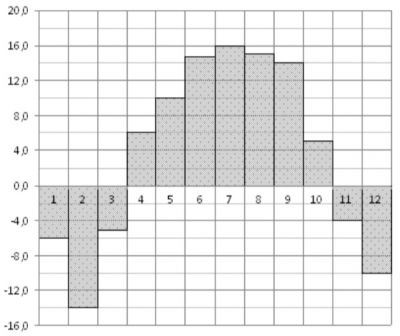
\(\boxed{2}\) На диаграмме показана среднемесячная температура воздуха в городе N за каждый месяц 1856 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме, на сколько градусов Цельсия во втором полугодии наибольшая среднемесячная температура превышала наименьшую.
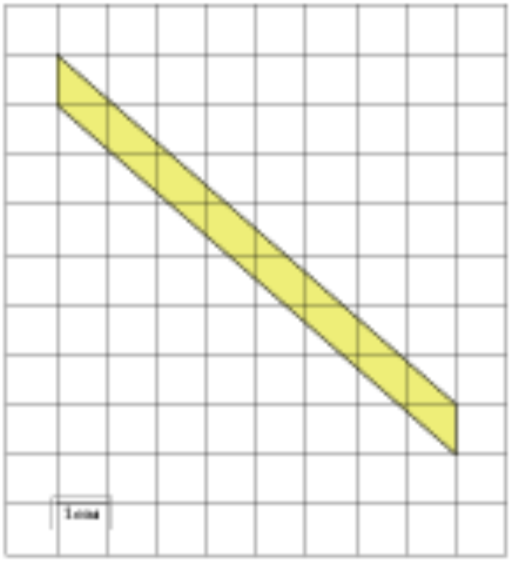
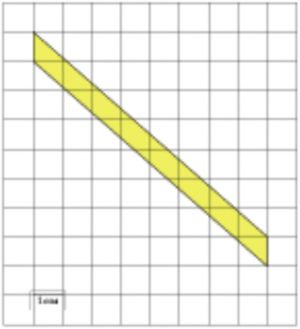
\(\boxed{3}\) Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
\(\boxed{4}\) Из множества чисел от 43 до 67 случайным образом выбирают одно число. Какова вероятность, что оно делится на 2?
\(\boxed{5}\) Решите уравнение \( \left( \dfrac{1}{13} \right)^{6x+7}=\dfrac{1}{169^{x-2}}\).
\(\boxed{6}\) Точки \(A\), \(B\), \(C\), \(D\), расположенные на окружности, делят эту окружность на четыре дуги \(AB\), \(BC\), \(CD\) и \(AD\), градусные величины которых относятся соответственно как \(1 : 3 : 14 : 18\). Найдите угол \(BAD\). Ответ дайте в градусах.
\(\boxed{7}\) Прямая \( y=-9x+5\) является касательной к графику функции \( y=ax^2+15x+11 \). Найдите \(a\).
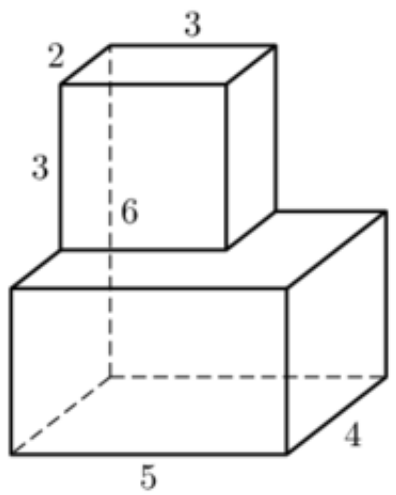
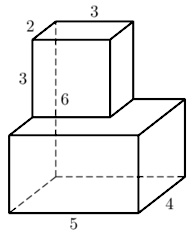
\(\boxed{8}\) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
\(\boxed{9}\) Найдите значение выражения \(2\cos(4\pi+\alpha)+5\sin\left( -\dfrac{\pi}2+\alpha\right) \), если \( \cos \alpha=\dfrac23\).
\(\boxed{10}\) Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле \( A( \omega)=\dfrac{A_0\omega_p^2}{\vert \omega_p^2-\omega^2 \vert} \), где \( \omega \) – частота вынуждающей силы (в \(с^{−1}\)), \(A_0\) – постоянный параметр, \( \omega_p=338\, с^{-1}\) – резонансная частота. Найдите максимальную частоту \( \omega\), меньшую резонансной, для которой амплитуда колебаний превосходит величину \(A_0\) не более чем на \(5{,}625\%\). Ответ выразите в \(с^{−1}\).
\(\boxed{11}\) Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 12 км/ч, а вторую половину пути – со скоростью 90 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 50 км/ч. Ответ дайте в км/ч.
\(\boxed{12}\) Найдите точку максимума функции \( y=(4x-6)\cos x-4\sin x+38 \) принадлежащую промежутку \(\left(0;\dfrac{\pi}{2}\right)\).
Магазин закупает подсвечники по оптовой цене 150 рублей за штуку и продает с наценкой 30%. Какое наибольшее количество таких подсвечников можно купить в этом магазине на 1800 рублей?
На диаграмме показана среднемесячная температура воздуха в городе N за каждый месяц 1856 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме, на сколько градусов Цельсия во втором полугодии наибольшая среднемесячная температура превышала наименьшую.
Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Из множества чисел от 43 до 67 случайным образом выбирают одно число. Какова вероятность, что оно делится на 2?
Решите уравнение \( \left( \dfrac{1}{13} \right)^{6x+7}=\dfrac{1}{169^{x-2}}\).
Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 1:3:14:18. Найдите угол BAD. Ответ дайте в градусах.
Прямая \( y=-9x+5\) является касательной к графику функции \( y=ax^2+15x+11 \). Найдите \(a\).
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Найдите значение выражения \(2\cos(4\pi+\alpha)+5\sin\left( -\dfrac{\pi}2+\alpha\right) \), если \( \cos \alpha=\dfrac23\).
Амплитуда колебаний маятника зависит от частоты вынуждающей силы и определяется по формуле \( A( \omega)=\dfrac{A_0\omega_p^2}{\vert \omega_p^2-\omega^2 \vert} \), где \( \omega \) – частота вынуждающей силы (в \(с^{−1}\)), \(A_0\) – постоянный параметр, \( \omega_p=338\, с^{-1}\) – резонансная частота. Найдите максимальную частоту \( \omega\), меньшую резонансной, для которой амплитуда колебаний превосходит величину \(A_0\) не более чем на \(5{,}625\%\). Ответ выразите в \(с^{−1}\).
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 12 км/ч, а вторую половину пути – со скоростью 90 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 50 км/ч. Ответ дайте в км/ч.
Найдите точку максимума функции \( y=(4x-6)\cos x-4\sin x+38 \) принадлежащую промежутку \(\left(0;\dfrac{\pi}{2}\right)\).