ЕГЭ профиль #3.18 (1-12)

Таксист за месяц проехал 6000 км. Цена бензина 41 рубль за литр. Средний расход бензина на 100 км составляет 6 литров. Сколько рублей потратил​ таксист на бензин за этот месяц?

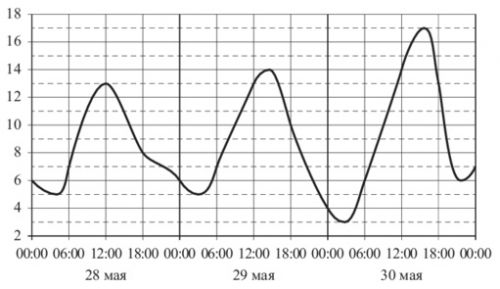
На рисунке показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали - значение температуры воздуха в градусах Цельсия. Определите порисунку наименьшую температуру воздуха 29 мая. Ответ дайте в градусах Цельсия.

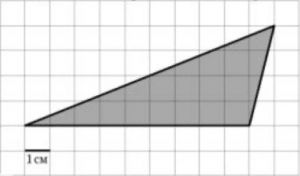
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.

Фабрика выпускает сумки. В среднем 9 сумок из 150 имеют скрытые дефекты. Найдите вероятность того, что купленная сумка окажется без дефектов.

Найдите корень уравнения: \(5^{x-12}=\dfrac{1}{125}\)

Площадь параллелограмма равна 140, две его стороны равны 10 и 35. Найдите большую высоту этого параллелограмма.

Прямая \(y =-3x-10\) параллельна касательной к графику функции \(y= x^2+5x+8\). Найдите абсциссу точки касания.

Найдите площадь поверхности многогранника (все двугранные углы прямые).

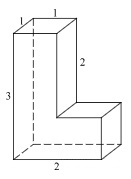
Найдите значение выражения \(4^{3{,}5}·5^{2{,}5}:20^{1{,}5}\)

После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле \(h=5t^2\) , где h — расстояние в метрах, t —время падения в секундах. До дождя время падения камешков составляло 1,5 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,1 с?

Велосипедист выехал с постоянной скоростью из города А в город Б, расстояние между которыми равно 180 км. На следующий день он отправился обратно со скоростью на 8 км/ч больше прежней. По дороге он сделал остановку на 8 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в Б. Найдите скорость велосипедиста на пути из А в Б. Ответ дайте в км/ч.

Найдите наименьшее значение функции \(y = 109\cos{x}- 115x + 61\) на отрезке \(\left[-\dfrac{3\pi}{2};0\right]\)