24.4. Окружности (Задачи ОГЭ)

Окружности с цен­тра­ми в точ­ках A и B пе­ре­се­ка­ют­ся в точ­ках C и D, причём точки A и B лежат по одну сто­ро­ну от пря­мой CD. Докажите, что CD ⊥ AB.

Докажите, что если окружность касается сторон AB и AC треугольника ABC в точках B и C, и биссектриса AD угла BAC пересекает меньшую из двух дуг BC в точке N, то CN — биссектриса угла ACB.

Дан правильный шестиугольник ABCDEF. Докажите, что угол ACD прямой.

В окруж­но­сти через се­ре­ди­ну O хорды AC про­ве­де­на хорда BD так, что дуги AB и CD равны. Докажите, что O — середина хорды BD.

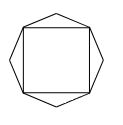
Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.