Группа №902

На координатной прямой отмечено число \(c\). Расположите в порядке возрастания числа \(c, c^2, \dfrac1{c}\).

Выберите верный вариант:
1. \(c, c^2, \dfrac1{c}\)
2. \(c^2, c, \dfrac1{c}\)
3. \(c, \dfrac1{c}, c^2 \)
4. \(\dfrac1{c}, c, c^2 \)

На координатной прямой отмечено число a.

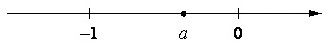
Расположите в порядке возрастания числа \(a-1,\dfrac{1}{a},a\).

В ответе укажите номер правильного варианта.

1) \(a,\dfrac{1}{a},a-1\)

2) \(a,a-1,\dfrac{1}{a}\)

3) \(a-1,a,\dfrac{1}{a}\)

4) \(\dfrac{1}{a},a-1,a\)

Числа a и b отмечены точками на координатной прямой. Расположите в порядке убывания числа \( \dfrac{1}{a}, \dfrac{1}{b}\) и 1.

1) \(\dfrac{1}{a};\dfrac{1}{b};1\)

2) \(\dfrac{1}{b};\dfrac{1}{a};1\)

3) \(\dfrac{1}{b};1;\dfrac{1}{a}\)

4) \(\dfrac{1}{a};1;\dfrac{1}{b}\)

На координатной прямой отмечено число \(c\). Расположите в порядке убывания числа \(c, c^2\) и \(\dfrac{1}{c}\).

1) \(\dfrac{1}{c}; c; c^2\)

2) \(c;\dfrac{1}{c};c^2\)

3) \(c^2;c;\dfrac{1}{c}\)

4)\(\dfrac{1}{c};c^2;c\)

Числа \(x\) и \(y\) от­ме­че­ны точ­ка­ми на ко­ор­ди­нат­ной пря­мой. Рас­по­ло­жи­те в по­ряд­ке воз­рас­та­ния числа \(\dfrac{1}{x}\), \(\dfrac{1}{y}\) и \(1\).

В ответе укажите номер правильного варианта.

1) \(\dfrac{1}{y}\); \(\dfrac{1}{x}\); \(1\)

2) \(1\); \(\dfrac{1}{x}\); \(\dfrac{1}{y}\)

3) \(\dfrac{1}{x}\); \(\dfrac{1}{y}\); \(1\)

4) \(1\); \(\dfrac{1}{y}\); \(\dfrac{1}{x}\)