Задачи ЕГЭ профиль
- 1. Планиметрия
- 2. Векторы
- 3. Стереометрия
- 4. Классическое определение вероятности
- 5. Теория вероятностей
- 6. Уравнения
- 7. Нахождение значений выражений
- 8. Производная
- 9. Задачи прикладного содержания
- 10. Текстовые задачи
- 11. Графики функций
- 12. Исследование функций
- 13. Сложные уравнения
- 14. Стереометрия
- 15. Неравенства
- 16. Экономические задачи
- 17. Планиметрия
- 18. Параметры
- 19. Теория чисел
Группа №593
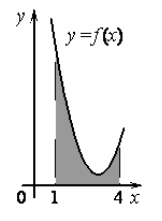
На рисунке изображён график некоторой функции \(y=f(x)\). Функция \(F(x) = \dfrac{1}{2}x^3-\dfrac{9}{2}x^2+14x-10\) - одна из первообразных функции \(f(x)\). Найдите площадь закрашенной фигуры.
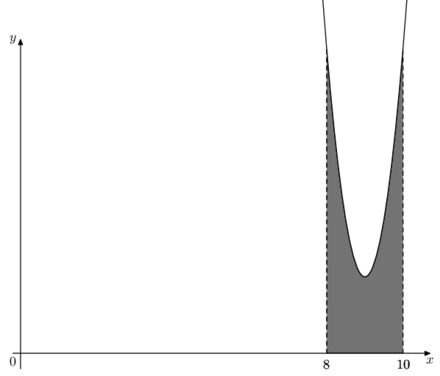
На рисунке избражен график функции \(f(x)\), одна из первообразных которой - \(F(x)=2x^3-54x^2+488x-\dfrac{3}{4}\). Найдите площадь закрашенной области.
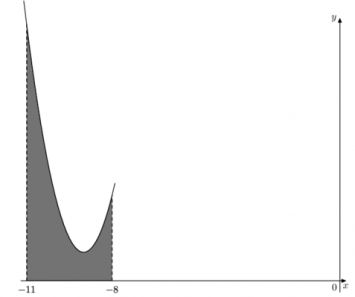
На рисунке изображён график некоторой функции \(y=f(x)\). Функция \(F(x)=x^3+30x^2+302x-\dfrac{15}{8}\) - одна из первообразных функции \(f(x)\). Найдите площадь закрашенной фигуры.
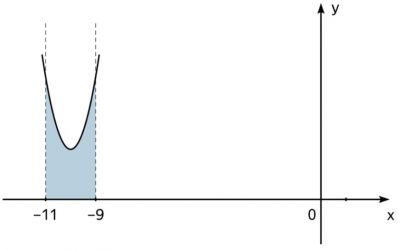
На рисунке избражен график функции \(f(x)\), одна из первообразных которой - \(F(x)=2x^3+36x^2+222x+\dfrac{7}{15}\). Найдите площадь закрашенной области.
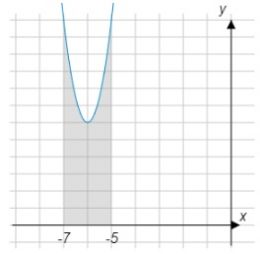
На рисунке изображён график некоторой функции \(y=f(x)\). Функция \(F(x) = \dfrac{1}{2}x^3+3x^2+\dfrac{15}{2}x+\dfrac{7}{2}\) - одна из первообразных функции \(f(x)\). Найдите площадь закрашенной фигуры.
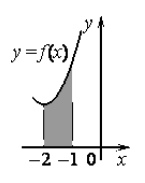
На рисунке изображен график некоторой функции \( y=f(x) \), одна из первообразных которой \( F(x)=\dfrac23 x^3 +10x^2+51x-\dfrac{13}{21} \). Найдите площадь закрашенной фигуры.
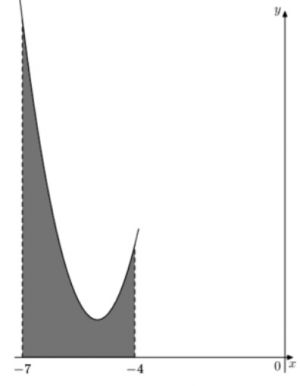
На рисунке изображен график некоторой функции \(y=f(x)\). Функция \(F(x)=\dfrac23 x^3+18x^2+163x+\dfrac3{14}\) – одна из первообразных функции \(f(x)\). Найдите площадь закрашенной фигуры.